2 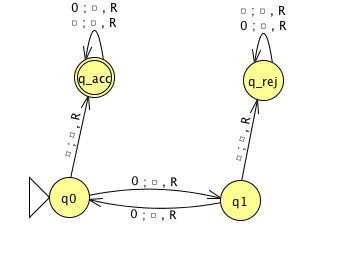
Formal definition:
Sample computation:
| \(q0\downarrow\) | ||||||
|---|---|---|---|---|---|---|
| \(0\) | \(0\) | \(0\) | \(\textvisiblespace\) | \(\textvisiblespace\) | \(\textvisiblespace\) | \(\textvisiblespace\) |
We are ready to introduce a formal model that will capture a notion of general purpose computation.
Similar to DFA, NFA, PDA: input will be an arbitrary string over a fixed alphabet.
Different from NFA, PDA: machine is deterministic.
Different from DFA, NFA, PDA: read-write head can move both to the left and to the right, and can extend to the right past the original input.
Similar to DFA, NFA, PDA: transition function drives computation one step at a time by moving within a finite set of states, always starting at designated start state.
Different from DFA, NFA, PDA: the special states for rejecting and accepting take effect immediately.
(See more details: Sipser p. 166)
Formally: a Turing machine is \(M= (Q, \Sigma, \Gamma, \delta, q_0, q_{accept}, q_{reject})\) where \(\delta\) is the transition function \[\delta: Q\times \Gamma \to Q \times \Gamma \times \{L, R\}\] The computation of \(M\) on a string \(w\) over \(\Sigma\) is:
Read/write head starts at leftmost position on tape.
Input string is written on \(|w|\)-many leftmost cells of tape, rest of the tape cells have the blank symbol. Tape alphabet is \(\Gamma\) with \(\textvisiblespace\in \Gamma\) and \(\Sigma \subseteq \Gamma\). The blank symbol \(\textvisiblespace \notin \Sigma\).
Given current state of machine and current symbol being read at the tape head, the machine transitions to next state, writes a symbol to the current position of the tape head (overwriting existing symbol), and moves the tape head L or R (if possible).
Computation ends if and when machine enters either the accept or the reject state. This is called halting. Note: \(q_{accept} \neq q_{reject}\).
The language recognized by the Turing machine \(M\), is \(L(M) = \{ w \in \Sigma^* \mid w \textrm{ is accepted by } M\}\), which is defined as \[\{ w \in \Sigma^* \mid \textrm{computation of $M$ on $w$ halts after entering the accept state}\}\]
2 
Formal definition:
Sample computation:
| \(q0\downarrow\) | ||||||
|---|---|---|---|---|---|---|
| \(0\) | \(0\) | \(0\) | \(\textvisiblespace\) | \(\textvisiblespace\) | \(\textvisiblespace\) | \(\textvisiblespace\) |
The language recognized by this machine is …
Describing Turing machines (Sipser p. 185) To define a Turing machine, we could give a
Formal definition: the \(7\)-tuple of parameters including set of states, input alphabet, tape alphabet, transition function, start state, accept state, and reject state; or,
Implementation-level definition: English prose that describes the Turing machine head movements relative to contents of tape, and conditions for accepting / rejecting based on those contents.
High-level description: description of algorithm (precise sequence of instructions), without implementation details of machine. As part of this description, can “call" and run another TM as a subroutine.
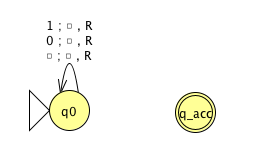
Fix \(\Sigma = \{0,1\}\), \(\Gamma = \{ 0, 1, \textvisiblespace\}\) for the Turing machines with the following state diagrams:
Example of string accepted:
Example of string rejected:
Implementation-level description
High-level description
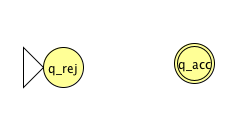
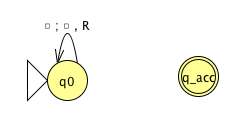
Example of string accepted:
Example of string rejected:
Implementation-level description
High-level description
Example of string accepted:
Example of string rejected:
Implementation-level description
High-level description
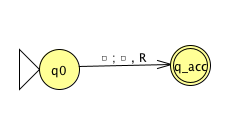
Example of string accepted:
Example of string rejected:
Implementation-level description
High-level description
Sipser Figure 3.10
Conventions in state diagram of TM: \(b \to R\) label means \(b \to b, R\) and all arrows missing from diagram represent transitions with output \((q_{reject}, \textvisiblespace , R)\)
2
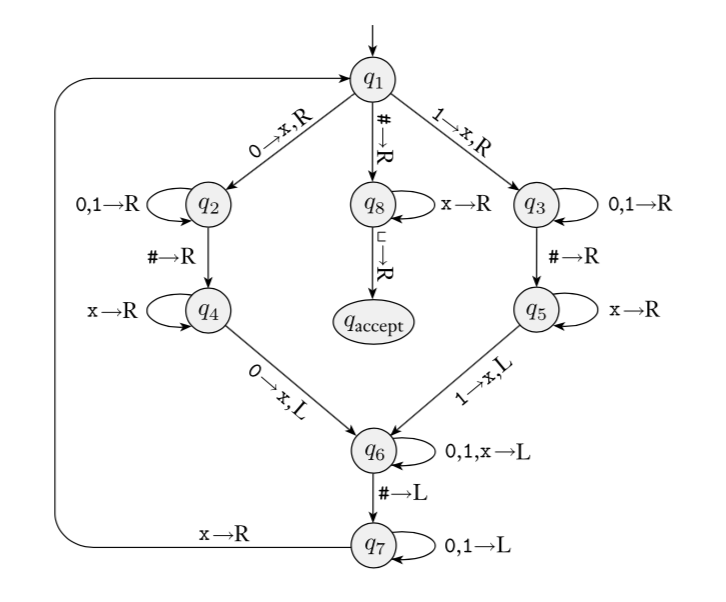
Implementation level description of this machine:
Zig-zag across tape to corresponding positions on either side of \(\#\) to check whether the characters in these positions agree. If they do not, or if there is no \(\#\), reject. If they do, cross them off.
Once all symbols to the left of the \(\#\) are crossed off, check for any un-crossed-off symbols to the right of \(\#\); if there are any, reject; if there aren’t, accept.
The language recognized by this machine is \[\{ w \# w \mid w \in \{0,1\}^* \}\]
Computation on input string \(01\#01\)
| \(q_1 \downarrow\) | ||||||
|---|---|---|---|---|---|---|
| \(0\) | \(1\) | \(\#\) | \(0\) | \(1\) | \(\textvisiblespace\) | \(\textvisiblespace\) |
2 High-level description of this machine is
Recall: High-level descriptions of Turing machine algorithms are written as indented text within quotation marks. Stages of the algorithm are typically numbered consecutively. The first line specifies the input to the machine, which must be a string.
Extra practice
Computation on input string \(01\#1\)
| \(q_1\downarrow\) | ||||||
|---|---|---|---|---|---|---|
| \(0\) | \(1\) | \(\#\) | \(1\) | \(\textvisiblespace\) | \(\textvisiblespace\) | \(\textvisiblespace\) |
A language \(L\) is recognized by a Turing machine \(M\) means
A Turing machine \(M\) recognizes a language \(L\) means
A Turing machine \(M\) is a decider means
A language \(L\) is decided by a Turing machine \(M\) means
A Turing machine \(M\) decides a language \(L\) means
Fix \(\Sigma = \{0,1\}\), \(\Gamma = \{ 0, 1, \textvisiblespace\}\) for the Turing machines with the following state diagrams:
 |
 |
| Decider? Yes / No | Decider? Yes / No |
 |
 |
| Decider? Yes / No | Decider? Yes / No |
A Turing-recognizable language is a set of strings that is the language recognized by some Turing machine. We also say that such languages are recognizable.
A Turing-decidable language is a set of strings that is the language recognized by some decider. We also say that such languages are decidable.
An unrecognizable language is a language that is not Turing-recognizable.
An undecidable language is a language that is not Turing-decidable.
True or False: Any decidable language is also recognizable.
True or False: Any recognizable language is also decidable.
True or False: Any undecidable language is also unrecognizable.
True or False: Any unrecognizable language is also undecidable.
True or False: The class of Turing-decidable languages is closed under complementation.
Using formal definition:
Using high-level description:
Church-Turing Thesis (Sipser p. 183): The informal notion of algorithm is formalized completely and correctly by the formal definition of a Turing machine. In other words: all reasonably expressive models of computation are equally expressive with the standard Turing machine.
Definition: A language \(L\) over an alphabet \(\Sigma\) is called co-recognizable if its complement, defined as \(\Sigma^* \setminus L = \{ x \in \Sigma^* \mid x \notin L \}\), is Turing-recognizable.
Theorem (Sipser Theorem 4.22): A language is Turing-decidable if and only if both it and its complement are Turing-recognizable.
Proof, first direction: Suppose language \(L\) is Turing-decidable. WTS that both it and its complement are Turing-recognizable.
Proof, second direction: Suppose language \(L\) is Turing-recognizable, and so is its complement. WTS that \(L\) is Turing-decidable.
Notation: The complement of a set \(X\) is denoted with a superscript \(c\), \(X^c\), or an overline, \(\overline{X}\).
Claim: If two languages (over a fixed alphabet \(\Sigma\)) are Turing-decidable, then their union is as well.
Proof:
Claim: If two languages (over a fixed alphabet \(\Sigma\)) are Turing-recognizable, then their union is as well.
Proof:
For Monday: Page 165-166 Introduction to Section 3.1
For Wednesday: Example 3.9 on page 173
For Friday: Page 184-185 Terminology for describing Turing machines
Use and design automata both formally and informally, including DFA, NFA, PDA, TM.
Use precise notation to formally define the state diagram of DFA, NFA, PDA, TM.
Use clear English to describe computations of DFA, NFA, PDA, TM informally
Determine whether a language is recognizable by a (D or N) FA and/or a PDA
Motivate the definition of a Turing machine
Trace the computation of a Turing machine on given input
Describe the language recognized by a Turing machine
Determine if a Turing machine is a decider
Given an implementation-level description of a Turing machine
Use high-level descriptions to define and trace Turing machines
Apply dovetailing in high-level definitions of machines
State and use the Church-Turing thesis
Classify the computational complexity of a set of strings by determining whether it is regular, context-free, decidable, or recognizable.
Give examples of sets that are regular, context-free, decidable, or recognizable.
Review quizzes based on class material each day.
Homework assignment 3 due this Thursday.
Project due next Thursday.