Recap so far: In DFA, the only memory available is in the states. Automata can only “remember” finitely far in the past and finitely much information, because they can have only finitely many states. If a computation path of a DFA visits the same state more than once, the machine can’t tell the difference between the first time and future times it visits this state. Thus, if a DFA accepts one long string, then it must accept (infinitely) many similar strings.
Definition A positive integer \(p\) is a pumping length of a language \(L\) over \(\Sigma\) means that, for each string \(s \in \Sigma^*\), if \(|s| \geq p\) and \(s \in L\), then there are strings \(x,y,z\) such that \[s = xyz\] and \[|y| > 0, \qquad \qquad \text{ for each $i \geq 0$, $xy^i z \in L$}, \qquad \text{and} \qquad \qquad |xy| \leq p.\]
Negation: A positive integer \(p\) is not a pumping length of a language \(L\) over \(\Sigma\) iff \[\exists s \left(~ |s| \geq p \wedge s \in L \wedge \forall x \forall y \forall z \left( ~\left( s = xyz \wedge |y| > 0 \wedge |xy| \leq p~ \right) \to \exists i ( i \geq 0 \wedge xy^iz \notin L ) \right) ~\right)\] Informally:
Restating Pumping Lemma: If \(L\) is a regular language, then it has a pumping length.
Contrapositive: If \(L\) has no pumping length, then it is nonregular.
The Pumping Lemma cannot be used to prove that a language is regular.
The Pumping Lemma can be used to prove that a language is not regular.
Extra practice: Exercise 1.49 in the book.
Proof strategy: To prove that a language \(L\) is not regular,
Consider an arbitrary positive integer \(p\)
Prove that \(p\) is not a pumping length for \(L\)
Conclude that \(L\) does not have any pumping length, and therefore it is not regular.
Example: \(\Sigma = \{0,1\}\), \(L = \{ 0^n 1^n \mid n \geq 0\}\).
Fix \(p\) an arbitrary positive integer. List strings that are in \(L\) and have length greater than or equal to \(p\):
Pick \(s =\)
Suppose \(s = xyz\) with \(|xy| \leq p\) and \(|y| > 0\).
Then when \(i = \hspace{1in}\), \(xy^i z = \hspace{1in}\)
Example: \(\Sigma = \{0,1\}\), \(L = \{w w^{\mathcal{R}} \mid w \in \{0,1\}^*\}\). Remember that the reverse of a string \(w\) is denoted \(w^\mathcal{R}\) and means to write \(w\) in the opposite order, if \(w = w_1 \cdots w_n\) then \(w^\mathcal{R} = w_n \cdots w_1\). Note: \(\varepsilon^\mathcal{R} = \varepsilon\).
Fix \(p\) an arbitrary positive integer. List strings that are in \(L\) and have length greater than or equal to \(p\):
Pick \(s =\)
Suppose \(s = xyz\) with \(|xy| \leq p\) and \(|y| > 0\).
Then when \(i = \hspace{1in}\), \(xy^i z = \hspace{1in}\)
Example: \(\Sigma = \{0,1\}\), \(L = \{0^j1^k \mid j \geq k \geq 0\}\).
Fix \(p\) an arbitrary positive integer. List strings that are in \(L\) and have length greater than or equal to \(p\):
Pick \(s =\)
Suppose \(s = xyz\) with \(|xy| \leq p\) and \(|y| > 0\).
Then when \(i = \hspace{1in}\), \(xy^i z = \hspace{1in}\)
Example: \(\Sigma = \{0,1\}\), \(L = \{0^n1^m0^n \mid m,n \geq 0\}\).
Fix \(p\) an arbitrary positive integer. List strings that are in \(L\) and have length greater than or equal to \(p\):
Pick \(s =\)
Suppose \(s = xyz\) with \(|xy| \leq p\) and \(|y| > 0\).
Then when \(i = \hspace{1in}\), \(xy^i z = \hspace{1in}\)
Extra practice:
| Language | \(s \in L\) | \(s \notin L\) | Is the language regular or nonregular? |
|---|---|---|---|
| \(\{a^nb^n \mid 0 \leq n \leq 5 \}\) | |||
| \(\{b^n a^n \mid n \geq 2\}\) | |||
| \(\{a^m b^n \mid 0 \leq m\leq n\}\) | |||
| \(\{a^m b^n \mid m \geq n+3, n \geq 0\}\) | |||
| \(\{b^m a^n \mid m \geq 1, n \geq 3\}\) | |||
| \(\{ w \in \{a,b\}^* \mid w = w^\mathcal{R} \}\) | |||
| \(\{ ww^\mathcal{R} \mid w\in \{a,b\}^* \}\) | |||
Regular sets are not the end of the story
Many nice / simple / important sets are not regular
Limitation of the finite-state automaton model: Can’t “count", Can only remember finitely far into the past, Can’t backtrack, Must make decisions in “real-time"
We know actual computers are more powerful than this model...
The next model of computation. Idea: allow some memory of unbounded size. How?
To generalize regular expressions: context-free
grammars
To generalize NFA: Pushdown automata, which is like an NFA with access to a stack: Number of states is fixed, number of entries in stack is unbounded. At each step (1) Transition to new state based on current state, letter read, and top letter of stack, then (2) (Possibly) push or pop a letter to (or from) top of stack. Accept a string iff there is some sequence of states and some sequence of stack contents which helps the PDA processes the entire input string and ends in an accepting state.
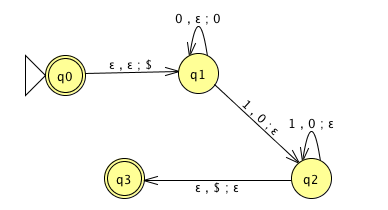
Is there a PDA that recognizes the nonregular language \(\{0^n1^n \mid n \geq 0 \}\)?

The PDA with state diagram above can be informally described as:
Read symbols from the input. As each 0 is read, push it onto the stack. As soon as 1s are seen, pop a 0 off the stack for each 1 read. If the stack becomes empty and we are at the end of the input string, accept the input. If the stack becomes empty and there are 1s left to read, or if 1s are finished while the stack still contains 0s, or if any 0s appear in the string following 1s, reject the input.
Trace the computation of this PDA on the input string \(01\).
Trace the computation of this PDA on the input string \(011\).
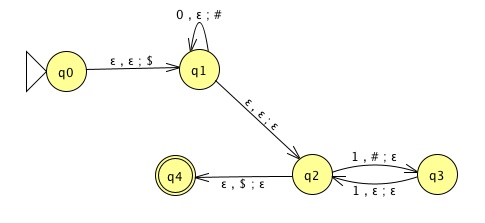
A PDA recognizing the set \(\{ \hspace{1.5 in} \}\) can be informally described as:
Read symbols from the input. As each 0 is read, push it onto the stack. As soon as 1s are seen, pop a 0 off the stack for each 1 read. If the stack becomes empty and there is exactly one 1 left to read, read that 1 and accept the input. If the stack becomes empty and there are either zero or more than one 1s left to read, or if the 1s are finished while the stack still contains 0s, or if any 0s appear in the input following 1s, reject the input.
Modify the state diagram below to get a PDA that implements this description:

Definition A pushdown automaton (PDA) is specified by a \(6\)-tuple \((Q, \Sigma, \Gamma, \delta, q_0, F)\) where \(Q\) is the finite set of states, \(\Sigma\) is the input alphabet, \(\Gamma\) is the stack alphabet, \[\delta: Q \times \Sigma_\varepsilon \times \Gamma_\varepsilon \to \mathcal{P}( Q \times \Gamma_\varepsilon)\] is the transition function, \(q_0 \in Q\) is the start state, \(F \subseteq Q\) is the set of accept states.
Draw the state diagram and give the formal definition of a PDA with \(\Sigma = \Gamma\).
Draw the state diagram and give the formal definition of a PDA with \(\Sigma \cap \Gamma = \emptyset\).
For the PDA state diagrams below, \(\Sigma = \{0,1\}\).
| Mathematical description of language | State diagram of PDA recognizing language |
|---|---|
| \(\Gamma = \{ \$, \#\}\) | |
 |
|
| \(\Gamma = \{ {@}, 1\}\) | |
 |
|
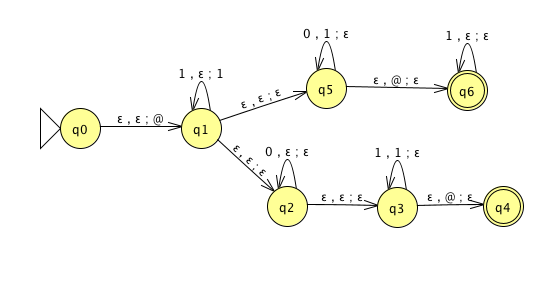
| \(\{ 0^i 1^j 0^k \mid i,j,k \geq 0 \}\) | |
Note: alternate notation is to replace \(;\) with \(\to\)
Big picture: PDAs were motivated by wanting to add some memory of unbounded size to NFA. How do we accomplish a similar enhancement of regular expressions to get a syntactic model that is more expressive?
DFA, NFA, PDA: Machines process one input string at a time; the computation of a machine on its input string reads the input from left to right.
Regular expressions: Syntactic descriptions of all strings that match a particular pattern; the language described by a regular expression is built up recursively according to the expression’s syntax
Context-free grammars: Rules to produce one string at a time, adding characters from the middle, beginning, or end of the final string as the derivation proceeds.
For Monday: Example 1.75, Example 1.77
For Wednesday: Definition 2.13 (page 111-112)
For Friday: Example 2.18 (page 114)
For Week 5 Monday: Introduction to Section 2.1 (page 102)
Classify the computational complexity of a set of strings by determining whether it is regular
Explain the limits of the class of regular languages
Identify some nonregular sets
Use the pumping lemma to prove that a given language is not regular.
Justify why the Pumping Lemma is true
Apply the Pumping Lemma in proofs of nonregularity
Use precise notation to formally define the state diagram of PDA and use clear English to describe computations of PDA informally.
Define push-down automata informally and formally
Trace the computation of a push-down automaton
Determine the language recognized by a given PDA
Design push-down automata to recognize specific languages
Determine whether a language is recognizable by a (D or N) FA and/or a PDA
Review quizzes based on class material each day.
Homework assignment 2 due Thursday.
Test next week on Friday in Discussion section.