In Computer Science, we operationalize “hardest” as “requires most resources”, where resources might be memory, time, parallelism, randomness, power, etc. To be able to compare “hardness” of problems, we use a consistent description of problems
Input: String
Output: Yes/ No, where Yes means that the input string matches the pattern or property described by the problem.
So far: we saw that regular expressions are convenient ways of describring patterns in strings. Finite automata give a model of computation for processing strings and and classifying them into Yes (accepted) or No (rejected). We will see that each set of strings is described by a regular expression if and only if there is a FA that recognizes it. Another way of thinking about it: properties described by regular expressions require exactly the computational power of these finite automata.
Review: Formal definition of finite automaton: \(M = (Q, \Sigma, \delta, q_0, F)\)
2
Finite set of states \(Q\)
Alphabet \(\Sigma\)
Transition function \(\delta\)
Start state \(q_0\)
Accept (final) states \(F\)
In the state diagram of \(M\), how many outgoing arrows are there from each state?
\(M = ( \{ q, r, s\}, \{a,b\}, \delta, q, \{q\} )\) where \(\delta\) is (rows labelled by states and columns labelled by symbols):
| \(\delta\) | \(a\) | \(b\) |
|---|---|---|
| \(q\) | \(r\) | \(r\) |
| \(r\) | \(s\) | \(s\) |
| \(s\) | \(q\) | \(q\) |
The state diagram for \(M\) is
Give two examples of strings that are accepted by \(M\) and two examples of strings that are rejected by \(M\):
\(L(M) =\)
A regular expression describing \(L(M)\) is
Let the alphabet be \(\Sigma_1 = \{0,1\}\).
A state diagram for a finite automaton that recognizes \(\{w \in \Sigma_1^* \mid w~\text{contains at most two $1$'s} \}\) is
A state diagram for a finite automaton that recognizes \(\{w \in \Sigma_1^* \mid w~\text{contains more than two $1$'s} \}\) is
Strategy: Add “labels" for states in the state diagram, e.g. “have not seen any of desired pattern yet” or “sink state”. Then, we can use the analysis of the roles of the states in the state diagram to work towards a description of the language recognized by the finite automaton.
A useful bit of terminology: the iterated transition function of a finite automaton \(M = (Q, \Sigma, \delta, q_0, F)\) is defined recursively by \[\delta^* (~(q,w)~) =\begin{cases} q \qquad &\text{if $q \in Q, w = \varepsilon$} \\ \delta( ~(q,a)~) \qquad &\text{if $q \in Q$, $w = a \in \Sigma$ } \\ \delta(~(\delta^*(q,u), a) ~) \qquad &\text{if $q \in Q$, $w = ua$ where $u \in \Sigma^*$ and $a \in \Sigma$} \end{cases}\]
Using this terminology, \(M\) accepts a string \(w\) over \(\Sigma\) if and only if \(\delta^*( ~(q_0,w)~) \in F\).
Suppose \(A\) is a language over an alphabet \(\Sigma\). By definition, this means \(A\) is a subset of \(\Sigma^*\). Claim: if there is a DFA \(M\) such that \(L(M) = A\) then there is another DFA, let’s call it \(M'\), such that \(L(M') = \overline{A}\), the complement of \(A\), defined as \(\{ w \in \Sigma^* \mid w \notin A \}\).
Proof idea:
Proof:
Application: Design a finite automaton that recognizes the language of all strings over \(\{a,b\}\) whose length is not a multiple of \(3\).
Note: On Friday, we’ll see a new kind of finite automaton. It will be helpful to distinguish it from the machines we’ve been talking about so we’ll use Deterministic Finite Automaton (DFA) to refer to the machines from Section 1.1.
| Nondeterministic finite automaton (Sipser Page 53) Given as \(M = (Q, \Sigma, \delta, q_0, F)\) | |
| Finite set of states \(Q\) | Can be labelled by any collection of distinct names. Default: \(q0, q1, \ldots\) |
| Alphabet \(\Sigma\) | Each input to the automaton is a string over \(\Sigma\). |
| Arrow labels \(\Sigma_\varepsilon\) | \(\Sigma_\varepsilon = \Sigma \cup \{ \varepsilon\}\). |
| Arrows in the state diagram are labelled either by symbols from \(\Sigma\) or by \(\varepsilon\) | |
| Transition function \(\delta\) | \(\delta: Q \times \Sigma_{\varepsilon} \to \mathcal{P}(Q)\) gives the set of possible next states for a transition |
| from the current state upon reading a symbol or spontaneously moving. | |
| Start state \(q_0\) | Element of \(Q\). Each computation of the machine starts at the start state. |
| Accept (final) states \(F\) | \(F \subseteq Q\). |
| \(M\) accepts the input string \(w \in \Sigma^*\) if and only if there is a computation of \(M\) on \(w\) that processes the whole string and ends in an accept state. | |
The formal definition of the NFA over \(\{0,1\}\) given by this state diagram is:

The language over \(\{0,1\}\) recognized by this NFA is:
Change the transition function to get a different NFA which accepts the empty string (and potentially other strings too).
The state diagram of an NFA over \(\{a,b\}\) is below. The formal definition of this NFA is:
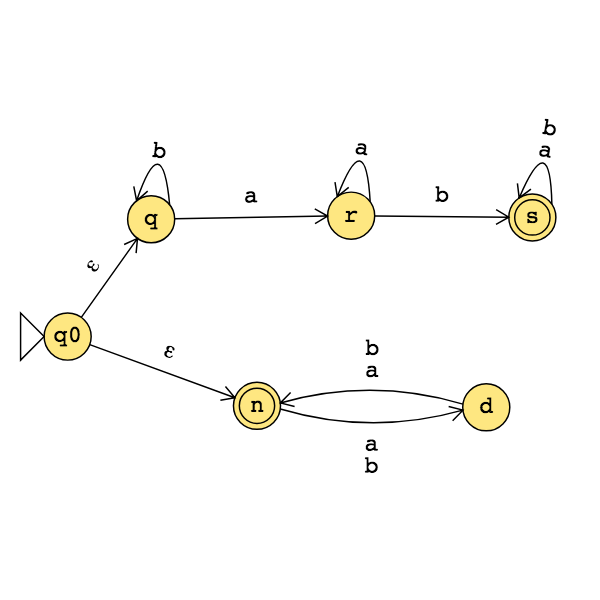
The language recognized by this NFA is:
For Wednesday: Pages 41-43 (Figures 1.18, 1.19, 1.20) (examples of automata and languages).
For Friday: Pages 48-50 (Figures 1.27, 1.29) (introduction to nondeterminism).
For Week 3 Monday: Pages 60-61 Theorem 1.47 and Theorem 1.48 (closure proofs).
Use regular expressions and relate them to languages and automata
Write and debug regular expressions using correct syntax
Use precise notation to formally define the state diagram of DFA, NFA and use clear English to describe computations of DFA, NFA informally.
Design an automaton that recognizes a given language
Specify a general construction for DFA based on parameters
Design general constructions for DFA
Motivate the use of nondeterminism
Trace the computation(s) of a nondeterministic finite automaton
#FinAid Assignment on Canvas https://canvas.ucsd.edu/courses/51649/quizzes/158899
Review quizzes based on class material each day.
Homework assignment 1 due Thursday.