 |
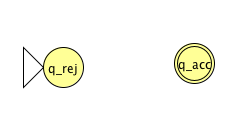 |
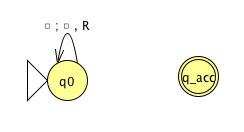
| Decider? Yes / No | Decider? Yes / No |
 |
 |
| Decider? Yes / No | Decider? Yes / No |
Nondeterministic Turing machine
At any point in the computation, the nondeterministic machine may proceed according to several possibilities: \((Q, \Sigma, \Gamma, \delta, q_0, q_{acc}, q_{rej})\) where \[\delta: Q \times \Gamma \to \mathcal{P}(Q \times \Gamma \times \{L, R\})\] The computation of a nondeterministic Turing machine is a tree with branching when the next step of the computation has multiple possibilities. A nondeterministic Turing machine accepts a string exactly when some branch of the computation tree enters the accept state.
Given a nondeterministic machine, we can use a \(3\)-tape Turing machine to simulate it by doing a breadth-first search of computation tree: one tape is “read-only” input tape, one tape simulates the tape of the nondeterministic computation, and one tape tracks nondeterministic branching. Sipser page 178
Two models of computation are called equally expressive when every language recognizable with the first model is recognizable with the second, and vice versa.
Church-Turing Thesis (Sipser p. 183): The informal notion of algorithm is formalized completely and correctly by the formal definition of a Turing machine. In other words: all reasonably expressive models of computation are equally expressive with the standard Turing machine.
A language \(L\) is recognized by a Turing machine \(M\) means
A Turing machine \(M\) recognizes a language \(L\) if means
A Turing machine \(M\) is a decider means
A language \(L\) is decided by a Turing machine \(M\) means
A Turing machine \(M\) decides a language \(L\) means
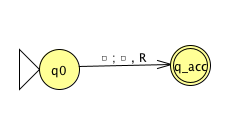
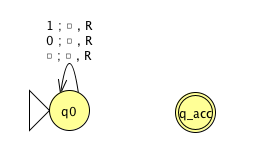
Fix \(\Sigma = \{0,1\}\), \(\Gamma = \{ 0, 1, \textvisiblespace\}\) for the Turing machines with the following state diagrams:
 |
 |
| Decider? Yes / No | Decider? Yes / No |
 |
 |
| Decider? Yes / No | Decider? Yes / No |
Claim: If two languages (over a fixed alphabet \(\Sigma\)) are Turing-recognizable, then their union is as well.
Proof using Turing machines:
Proof using nondeterministic Turing machines:
Proof using enumerators:
Describing Turing machines (Sipser p. 185)
To define a Turing machine, we could give a
Formal definition: the \(7\)-tuple of parameters including set of states, input alphabet, tape alphabet, transition function, start state, accept state, and reject state; or,
Implementation-level definition: English prose that describes the Turing machine head movements relative to contents of tape, and conditions for accepting / rejecting based on those contents.
High-level description: description of algorithm (precise sequence of instructions), without implementation details of machine. As part of this description, can “call" and run another TM as a subroutine.
The Church-Turing thesis posits that each algorithm can be implemented by some Turing machine
High-level descriptions of Turing machine algorithms are written as indented text within quotation marks.
Stages of the algorithm are typically numbered consecutively.
The first line specifies the input to the machine, which must be a string. This string may be the encoding of some object or list of objects.
Notation: \(\langle O \rangle\) is the string that encodes the object \(O\). \(\langle O_1, \ldots, O_n \rangle\) is the string that encodes the list of objects \(O_1, \ldots, O_n\).
Assumption: There are Turing machines that can be called as subroutines to decode the string representations of common objects and interact with these objects as intended (data structures).
For example, since there are algorithms to answer each of the following questions, by Church-Turing thesis, there is a Turing machine that accepts exactly those strings for which the answer to the question is “yes”
Does a string over \(\{0,1\}\) have even length?
Does a string over \(\{0,1\}\) encode a string of ASCII characters?1
Does a DFA have a specific number of states?
Do two NFAs have any state names in common?
Do two CFGs have the same start variable?