Monday

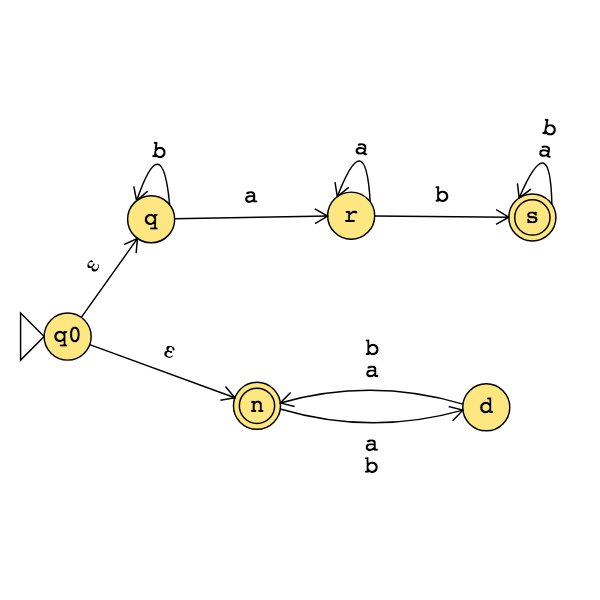
The state diagram of an NFA over $\{a,b\}$ is below. The formal definition of this NFA is:

The language recognized by this NFA is:

Suppose $A_1, A_2$ are languages over an alphabet $\Sigma$. Claim: if there is a NFA $N_1$ such that $L(N_1) = A_1$ and NFA $N_2$ such that $L(N_2) = A_2$, then there is another NFA, let’s call it $N$, such that $L(N) = A_1 \cup A_2$.

Proof idea: Use nondeterminism to choose which of $N_1$, $N_2$ to run.

Formal construction: Let $N_1 = (Q_1, \Sigma, \delta_1, q_1, F_1)$ and $N_2 = (Q_2, \Sigma, \delta_2,q_2, F_2)$ and assume $Q_1 \cap Q_2 = \emptyset$ and that $q_0 \notin Q_1 \cup Q_2$. Construct $N = (Q, \Sigma, \delta, q_0, F_1 \cup F_2)$ where

$Q =$
$\delta: Q \times \Sigma_\varepsilon \to \mathcal{P}(Q)$ is defined by, for $q \in Q$ and $a \in \Sigma_{\varepsilon}$: \[\phantom{\delta((q,a))=\begin{cases} \delta_1 ((q,a)) &\qquad\text{if } q\in Q_1 \\ \delta_2 ((q,a)) &\qquad\text{if } q\in Q_2 \\ \{q1,q2\} &\qquad\text{if } q = q_0, a = \varepsilon \\ \emptyset\text{if } q= q_0, a \neq \varepsilon \end{cases}}\]

Proof of correctness would prove that $L(N) = A_1 \cup A_2$ by considering an arbitrary string accepted by $N$, tracing an accepting computation of $N$ on it, and using that trace to prove the string is in at least one of $A_1$, $A_2$; then, taking an arbitrary string in $A_1 \cup A_2$ and proving that it is accepted by $N$. Details left for extra practice.

Over the alphabet $\{a,b\}$, the language $L$ described by the regular expression $\Sigma^* a \Sigma^* b$

includes the strings and excludes the strings

The state diagram of a NFA recognizing $L$ is:

Proof idea: Allow computation to move between $N_1$ and $N_2$ “spontaneously" when reach an accepting state of $N_1$, guessing that we’ve reached the point where the two parts of the string in the set-wise concatenation are glued together.

Formal construction: Let $N_1 = (Q_1, \Sigma, \delta_1, q_1, F_1)$ and $N_2 = (Q_2, \Sigma, \delta_2,q_2, F_2)$ and assume $Q_1 \cap Q_2 = \emptyset$. Construct $N = (Q, \Sigma, \delta, q_0, F)$ where

$Q =$
$q_0 =$
$F =$
$\delta: Q \times \Sigma_\varepsilon \to \mathcal{P}(Q)$ is defined by, for $q \in Q$ and $a \in \Sigma_{\varepsilon}$: \[\delta((q,a))=\begin{cases} \delta_1 ((q,a)) &\qquad\text{if } q\in Q_1 \textrm{ and } q \notin F_1\\ \delta_1 ((q,a)) &\qquad\text{if } q\in F_1 \textrm{ and } a \in \Sigma\\ \delta_1 ((q,a)) \cup \{q_2\} &\qquad\text{if } q\in F_1 \textrm{ and } a = \varepsilon\\ \delta_2 ((q,a)) &\qquad\text{if } q\in Q_2 \end{cases}\]

Proof of correctness would prove that $L(N) = A_1 \circ A_2$ by considering an arbitrary string accepted by $N$, tracing an accepting computation of $N$ on it, and using that trace to prove the string can be written as the result of concatenating two strings, the first in $A_1$ and the second in $A_2$; then, taking an arbitrary string in $A_1 \circ A_2$ and proving that it is accepted by $N$. Details left for extra practice.

Suppose $A$ is a language over an alphabet $\Sigma$. Claim: if there is a NFA $N$ such that $L(N) = A$, then there is another NFA, let’s call it $N'$, such that $L(N') = A^*$.

Proof idea: Add a fresh start state, which is an accept state. Add spontaneous moves from each (old) accept state to the old start state.

Formal construction: Let $N = (Q, \Sigma, \delta, q_1, F)$ and assume $q_0 \notin Q$. Construct $N' = (Q', \Sigma, \delta', q_0, F')$ where

$Q' = Q \cup \{q_0\}$
$F' = F \cup \{q_0\}$
$\delta': Q' \times \Sigma_\varepsilon \to \mathcal{P}(Q')$ is defined by, for $q \in Q'$ and $a \in \Sigma_{\varepsilon}$: \[\delta'((q,a))=\begin{cases} \delta ((q,a)) &\qquad\text{if } q\in Q \textrm{ and } q \notin F\\ \delta ((q,a)) &\qquad\text{if } q\in F \textrm{ and } a \in \Sigma\\ \delta ((q,a)) \cup \{q_1\} &\qquad\text{if } q\in F \textrm{ and } a = \varepsilon\\ \{q_1\} &\qquad\text{if } q = q_0 \textrm{ and } a = \varepsilon \\ \emptyset &\qquad\text{if } q = q_0 \textrm { and } a \in \Sigma \end{cases}\]

Proof of correctness would prove that $L(N') = A^*$ by considering an arbitrary string accepted by $N'$, tracing an accepting computation of $N'$ on it, and using that trace to prove the string can be written as the result of concatenating some number of strings, each of which is in $A$; then, taking an arbitrary string in $A^*$ and proving that it is accepted by $N'$. Details left for extra practice.

Application: A state diagram for a NFA over $\Sigma = \{a,b\}$ that recognizes $L (( \Sigma^* b)^* )$:

True or False: The state diagram of any DFA is also the state diagram of a NFA.

True or False: The state diagram of any NFA is also the state diagram of a DFA.

True or False: The formal definition $(Q, \Sigma, \delta, q_0, F)$ of any DFA is also the formal definition of a NFA.

True or False: The formal definition $(Q, \Sigma, \delta, q_0, F)$ of any NFA is also the formal definition of a DFA.

Review: Week 3 Monday

Recall: Review quizzes based on class material are assigned each day. These quizzes will help you track and confirm your understanding of the concepts and examples we work in class. Quizzes can be submitted on Gradescope as many times (with no penalty) as you like until the quiz deadline: the three quizzes each week are all due on Friday (with no penalty late submission open until Sunday).

Please complete the review quiz questions on Gradescope about constructions using NFAs.

Pre class reading for next time: Theorem 1.39 “Proof Idea”, Example 1.41, Example 1.56, Example 1.58.

Wednesday

Consider the state diagram of an NFA over $\{a,b\}$:

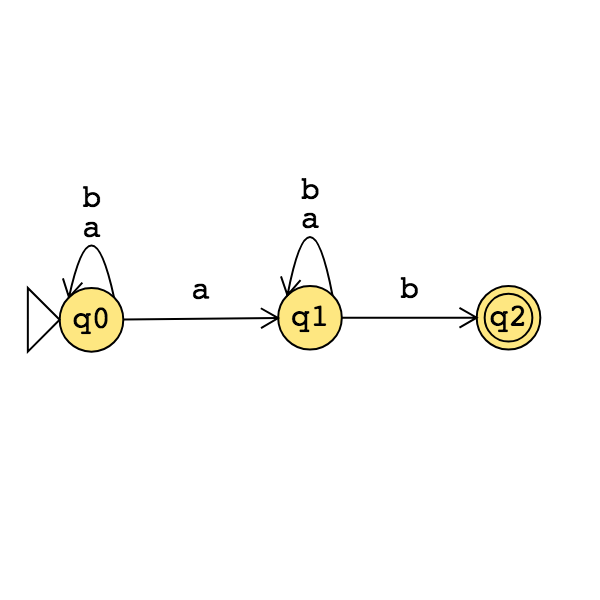
The language recognized by this NFA is

The state diagram of a DFA recognizing this same language is:

Suppose $A$ is a language over an alphabet $\Sigma$. Claim: if there is a NFA $N$ such that $L(N) = A$ then there is a DFA $M$ such that $L(M) = A$.

Proof idea: States in $M$ are “macro-states" – collections of states from $N$ – that represent the set of possible states a computation of $N$ might be in.

Formal construction: Let $N = (Q, \Sigma, \delta, q_0, F)$. Define \[M = (~ \mathcal{P}(Q), \Sigma, \delta', q', \{ X \subseteq Q \mid X \cap F \neq \emptyset \}~ )\] where $q' = \{ q \in Q \mid \text{$q = q_0$ or is accessible from $q_0$ by spontaneous moves in $N$} \}$ and \[\delta' (~(X, x)~) = \{ q \in Q \mid q \in \delta( ~(r,x)~) ~\text{for some $r \in X$ or is accessible from such an $r$ by spontaneous moves in $N$} \}\]

Consider the state diagram of an NFA over $\{0,1\}$. Use the “macro-state” construction to find an equivalent DFA.

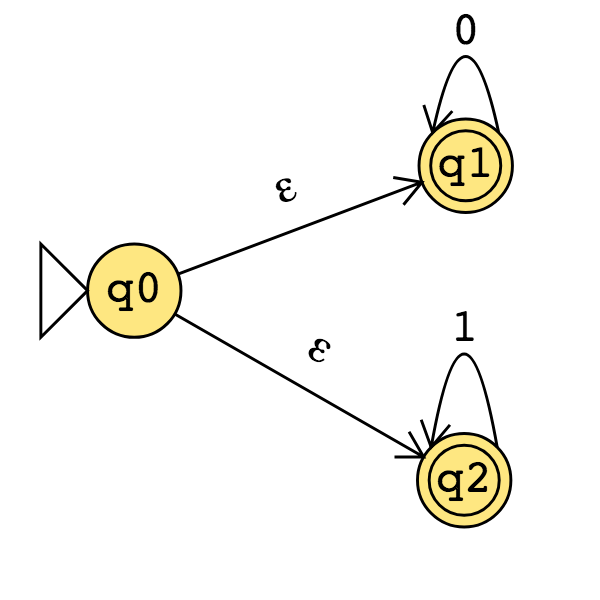
Prune this diagram to get an equivalent DFA with only the “macro-states" reachable from the start state.

Suppose $A$ is a language over an alphabet $\Sigma$. Claim: if there is a regular expression $R$ such that $L(R) = A$, then there is a NFA, let’s call it $N$, such that $L(N) = A$.

Structural induction: Regular expression is built from basis regular expressions using inductive steps (union, concatenation, Kleene star symbols). Use constructions to mirror these in NFAs.

Application: A state diagram for a NFA over $\{a,b\}$ that recognizes $L(a^* (ab)^*)$:

Suppose $A$ is a language over an alphabet $\Sigma$. Claim: if there is a DFA $M$ such that $L(M) = A$, then there is a regular expression, let’s call it $R$, such that $L(R) = A$.

Proof idea: Trace all possible paths from start state to accept state. Express labels of these paths as regular expressions, and union them all.

Add new start state with $\varepsilon$ arrow to old start state.
Add new accept state with $\varepsilon$ arrow from old accept states. Make old accept states non-accept.
Remove one (of the old) states at a time: modify regular expressions on arrows that went through removed state to restore language recognized by machine.

Application: Find a regular expression describing the language recognized by the DFA with state diagram

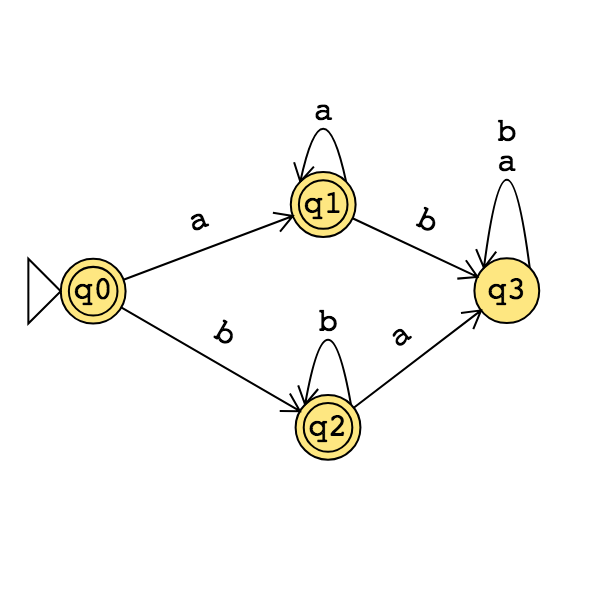
Conclusion: For each language $L$,

There is a DFA that recognizes $L$ $\exists M ~(M \textrm{ is a DFA and } L(M) = A)$
if and only if
There is a NFA that recognizes $L$ $\exists N ~(N \textrm{ is a NFA and } L(N) = A)$
if and only if
There is a regular expression that describes $L$ $\exists R ~(R \textrm{ is a regular expression and } L(R) = A)$

A language is called regular when any (hence all) of the above three conditions are met.

Review: Week 3 Wednesday

Please complete the review quiz questions on Gradescope about translating between DFA, NFA, and regular expressions.

Pre class reading for next time: Introduction to Section 1.4 (page 77)

Friday

Theorem: For an alphabet $\Sigma$, For each language $L$ over $\Sigma$,

$L$ is recognized by some DFA
iff
$L$ is recognized by some NFA
iff
$L$ is described by some regular expression

If (any, hence all) these conditions apply, $L$ is called regular.

Prove or Disprove: There is some alphabet $\Sigma$ for which there is some language recognized by an NFA but not by any DFA.

Prove or Disprove: There is some alphabet $\Sigma$ for which there is some finite language not described by any regular expression over $\Sigma$.

Prove or Disprove: If a language is recognized by an NFA then the complement of this language is not recognized by any DFA.

Set	Cardinality

$\{0,1\}$

$\{0,1\}^*$

$\mathcal{P}( \{0,1\})$

The set of all languages over $\{0,1\}$

The set of all regular expressions over $\{0,1\}$

The set of all regular languages over $\{0,1\}$

Pumping Lemma (Sipser Theorem 1.70): If $A$ is a regular language, then there is a number $p$ (a pumping length) where, if $s$ is any string in $A$ of length at least $p$, then $s$ may be divided into three pieces, $s = xyz$ such that

$|y| > 0$
for each $i \geq 0$, $xy^i z \in A$
$|xy| \leq p$.

True or False: A pumping length for $A = \{ 0,1 \}^*$ is $p = 5$.

True or False: A pumping length for $A = \{1, 01, 001, 0001, 00001 \}$ is $p = 4$.

True or False: A pumping length for $A = \{0^j 1 \mid j \geq 0 \}$ is $p = 3$.

True or False: For any language $A$, if $p$ is a pumping length for $A$ and $p' > p$, then $p'$ is also a pumping length for $A$.

Review: Week 3 Friday

Please complete the review quiz questions on Gradescope about the class of regular languages.

Pre class reading for next time: Example 1.75, Example 1.77

Set	Cardinality

\(\{0,1\}\)

\(\{0,1\}^*\)

\(\mathcal{P}( \{0,1\})\)

The set of all languages over \(\{0,1\}\)

The set of all regular expressions over \(\{0,1\}\)

The set of all regular languages over \(\{0,1\}\)