Week3 wednesday

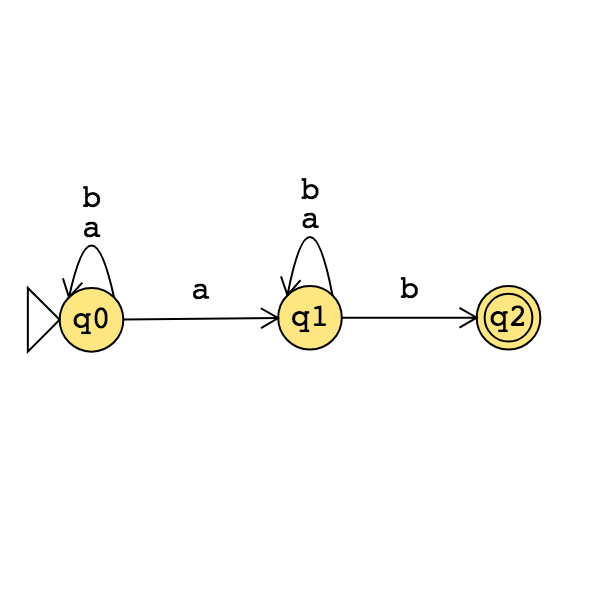
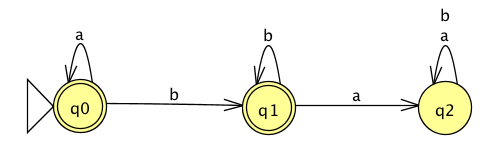
Consider the state diagram of an NFA over $\{a,b\}$:

The language recognized by this NFA is

The state diagram of a DFA recognizing this same language is:

Suppose $A$ is a language over an alphabet $\Sigma$. Claim: if there is a NFA $N$ such that $L(N) = A$ then there is a DFA $M$ such that $L(M) = A$.

Proof idea: States in $M$ are “macro-states" – collections of states from $N$ – that represent the set of possible states a computation of $N$ might be in.

Formal construction: Let $N = (Q, \Sigma, \delta, q_0, F)$. Define \[M = (~ \mathcal{P}(Q), \Sigma, \delta', q', \{ X \subseteq Q \mid X \cap F \neq \emptyset \}~ )\] where $q' = \{ q \in Q \mid \text{$q = q_0$ or is accessible from $q_0$ by spontaneous moves in $N$} \}$ and \[\delta' (~(X, x)~) = \{ q \in Q \mid q \in \delta( ~(r,x)~) ~\text{for some $r \in X$ or is accessible from such an $r$ by spontaneous moves in $N$} \}\]

Consider the state diagram of an NFA over $\{0,1\}$. Use the “macro-state” construction to find an equivalent DFA.

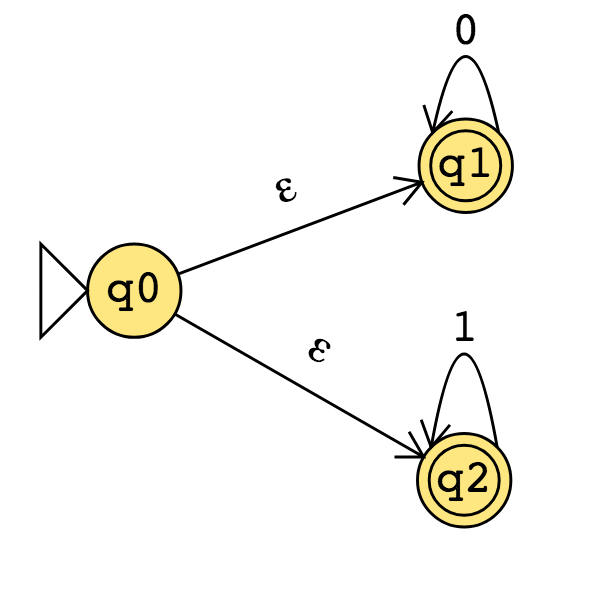
Prune this diagram to get an equivalent DFA with only the “macro-states" reachable from the start state.

Suppose $A$ is a language over an alphabet $\Sigma$. Claim: if there is a regular expression $R$ such that $L(R) = A$, then there is a NFA, let’s call it $N$, such that $L(N) = A$.

Structural induction: Regular expression is built from basis regular expressions using inductive steps (union, concatenation, Kleene star symbols). Use constructions to mirror these in NFAs.

Application: A state diagram for a NFA over $\{a,b\}$ that recognizes $L(a^* (ab)^*)$:

Suppose $A$ is a language over an alphabet $\Sigma$. Claim: if there is a DFA $M$ such that $L(M) = A$, then there is a regular expression, let’s call it $R$, such that $L(R) = A$.

Proof idea: Trace all possible paths from start state to accept state. Express labels of these paths as regular expressions, and union them all.

Add new start state with $\varepsilon$ arrow to old start state.
Add new accept state with $\varepsilon$ arrow from old accept states. Make old accept states non-accept.
Remove one (of the old) states at a time: modify regular expressions on arrows that went through removed state to restore language recognized by machine.

Application: Find a regular expression describing the language recognized by the DFA with state diagram

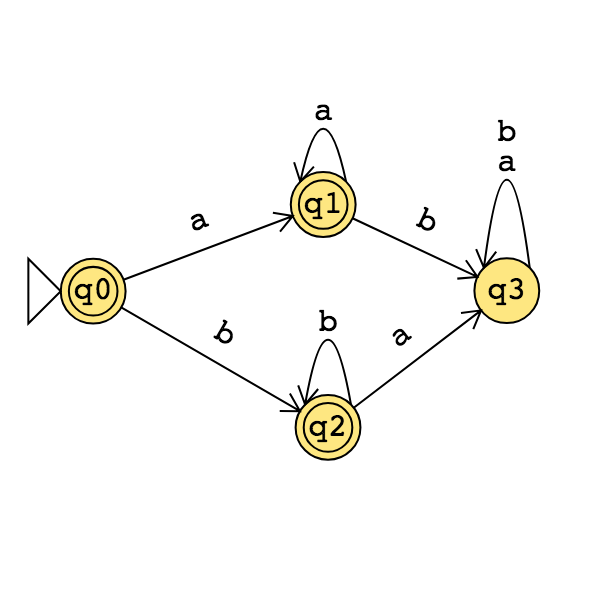
Conclusion: For each language $L$,

There is a DFA that recognizes $L$ $\exists M ~(M \textrm{ is a DFA and } L(M) = A)$
if and only if
There is a NFA that recognizes $L$ $\exists N ~(N \textrm{ is a NFA and } L(N) = A)$
if and only if
There is a regular expression that describes $L$ $\exists R ~(R \textrm{ is a regular expression and } L(R) = A)$

A language is called regular when any (hence all) of the above three conditions are met.

Week2 monday

Review: Formal definition of DFA: $M = (Q, \Sigma, \delta, q_0, F)$

Finite set of states $Q$
Alphabet $\Sigma$
Transition function $\delta$
Start state $q_0$
Accept (final) states $F$

In the state diagram of $M$, how many outgoing arrows are there from each state?

$M = ( \{ q, r, s\}, \{a,b\}, \delta, q, \{s\} )$ where $\delta$ is (rows labelled by states and columns labelled by symbols):

$\delta$	$a$	$b$
$q$	$r$	$q$
$r$	$r$	$s$
$s$	$s$	$s$

The state diagram for $M$ is

Give two examples of strings that are accepted by $M$ and two examples of strings that are rejected by $M$:

Add “labels" for states in the state diagram, e.g. “have not seen any of desired pattern yet” or “sink state”.

We can use the analysis of the roles of the states in the state diagram to describe the language recognized by the DFA.

$L(M) =$

A regular expression describing $L(M)$ is

Let the alphabet be $\Sigma_1 = \{0,1\}$.

A state diagram for a DFA that recognizes $\{w \mid w~\text{contains at most two $1$'s} \}$ is

A state diagram for a DFA that recognizes $\{w \mid w~\text{contains more than two $1$'s} \}$ is

Extra example: A state diagram for DFA recognizing \[\{w \mid w~\text{is a string over $\{0,1\}$ whose length is not a multiple of $3$} \}\]

Let $n$ be an arbitrary positive integer. What is a formal definition for a DFA recognizing \[\{w \mid w~\text{is a string over $\{0,1\}$ whose length is not a multiple of $n$} \}?\]

Week2 wednesday

Suppose A is a language over an alphabet $\Sigma$. By definition, this means A is a subset of $\Sigma^*$. Claim: if there is a DFA $M$ such that $L(M) = A$ then there is another DFA, let’s call it $M'$, such that $L(M') = \overline{A}$, the complement of $A$, defined as $\{ w \in \Sigma^* \mid w \notin A \}$.

Proof idea:

Proof:

A useful (optional) bit of terminology: the iterated transition function of a DFA $M = (Q, \Sigma, \delta, q_0, F)$ is defined recursively by \[\delta^* (~(q,w)~) =\begin{cases} q \qquad &\text{if $q \in Q, w = \varepsilon$} \\ \delta( ~(q,a)~) \qquad &\text{if $q \in Q$, $w = a \in \Sigma$ } \\ \delta(~(\delta^*(q,u), a) ~) \qquad &\text{if $q \in Q$, $w = ua$ where $u \in \Sigma^*$ and $a \in \Sigma$} \end{cases}\]

Using this terminology, $M$ accepts a string $w$ over $\Sigma$ if and only if $\delta^*( ~(q_0,w)~) \in F$.

Fix $\Sigma = \{a,b\}$. A state diagram for a DFA that recognizes $\{w \mid w~\text{has $ab$ as a substring and is of even length} \}$:

Suppose $A_1, A_2$ are languages over an alphabet $\Sigma$. Claim: if there is a DFA $M_1$ such that $L(M_1) = A_1$ and DFA $M_2$ such that $L(M_2) = A_2$, then there is another DFA, let’s call it $M$, such that $L(M) = A_1 \cap A_2$.

Proof idea:

Formal construction:

Application: When $A_1 = \{w \mid w~\text{has $ab$ as a substring} \}$ and $A_2 = \{ w \mid w~\text{is of even length} \}$.

Proof idea:

Formal construction:

Application: A state diagram for a DFA that recognizes $\{w \mid w~\text{has $ab$ as a substring or is of even length} \}$:

Week1 wednesday

Our motivation in studying sets of strings is that they encode problems.

We need to describe the collection of all strings that match the pattern or property of a problem.

Let’s start by thinking about how we can describe a language (a set of strings from a given alphabet).

Definition 1.52: A regular expression over alphabet $\Sigma$ is a syntactic expression that can describe a language over $\Sigma$. The collection of all regular expressions is defined recursively:

Basis steps of recursive definition

$a$ is a regular expression, for $a \in \Sigma$

$\varepsilon$ is a regular expression

$\emptyset$ is a regular expression
Recursive steps of recursive definition

$(R_1 \cup R_2)$ is a regular expression when $R_1$, $R_2$ are regular expressions

$(R_1 \circ R_2)$ is a regular expression when $R_1$, $R_2$ are regular expressions

$(R_1^*)$ is a regular expression when $R_1$ is a regular expression

The semantics (or meaning) of the syntactic regular expression is the language described by the regular expression. The function that assigns a language to a regular expression over $\Sigma$ is defined recursively, using familiar set operations:

Basis steps of recursive definition

The language described by $a$, for $a \in \Sigma$, is $\{a\}$ and we write $L(a) = \{a\}$

The language described by $\varepsilon$ is $\{\varepsilon\}$ and we write $L(\varepsilon) = \{ \varepsilon\}$

The language described by $\emptyset$ is $\{\}$ and we write $L(\emptyset) = \emptyset$.
Recursive steps of recursive definition

When $R_1$, $R_2$ are regular expressions, the language described by the regular expression $(R_1 \cup R_2)$ is the union of the languages described by $R_1$ and $R_2$, and we write \[L(~(R_1 \cup R_2)~) = L(R_1) \cup L(R_2) = \{ w \mid w \in L(R_1) \lor w \in L(R_2)\}\]

When $R_1$, $R_2$ are regular expressions, the language described by the regular expression $(R_1 \circ R_2)$ is the concatenation of the languages described by $R_1$ and $R_2$, and we write \[L(~(R_1 \circ R_2)~) = L(R_1) \circ L(R_2) = \{ uv \mid u \in L(R_1) \land v \in L(R_2)\}\]

When $R_1$ is a regular expression, the language described by the regular expression $(R_1^*)$ is the Kleene star of the language described by $R_1$ and we write \[L(~(R_1^*)~) = (~L(R_1)~)^* = \{ w_1 \cdots w_k \mid k \geq 0 \textrm{ and each } w_i \in L(R_1)\}\]

For the following examples assume the alphabet is $\Sigma_1 = \{0,1\}$:

The language described by the regular expression $0$ is $L(0) = \{ 0 \}$

The language described by the regular expression $1$ is $L(1) = \{ 1 \}$

The language described by the regular expression $\varepsilon$ is $L(\varepsilon) = \{ \varepsilon \}$

The language described by the regular expression $\emptyset$ is $L(\emptyset) = \emptyset$

The language described by the regular expression $((0 \cup 1) \cup 1)$ is $L(~((0 \cup 1) \cup 1)~) =$

The language described by the regular expression $1^+$ is $L(~(1)^+~) =$

The language described by the regular expression $\Sigma_1^* 1$ is $L(~\Sigma_1^* 1~) =$

The language described by the regular expression $(\Sigma_1 \Sigma_1 \Sigma_1 \Sigma_1 \Sigma_1)^*$ is $L(~(\Sigma_1 \Sigma_1 \Sigma_1 \Sigma_1 \Sigma_1)^*~) =$

A regular expression that describes the language $\{00, 01, 10, 11\}$ is

A regular expression that describes the language $\{ 0^n1 \mid n~\text{is even} \}$ is

Shorthand and conventions

Assuming $\Sigma$ is the alphabet, we use the following conventions
$\Sigma$	regular expression describing language consisting of all strings of length $1$ over $\Sigma$
$*$ then $\circ$ then $\cup$	precedence order, unless parentheses are used to change it
$R_1R_2$	shorthand for $R_1 \circ R_2$ (concatenation symbol is implicit)
$R^+$	shorthand for $R^* \circ R$
$R^k$	shorthand for $R$ concatenated with itself $k$ times, where $k$ is a natural number
Pages 63 - 65

Caution: many programming languages that support regular expressions build in functionality that is more powerful than the “pure” definition of regular expressions given here.

Regular expressions are everywhere (once you start looking for them).

Software tools and languages often have built-in support for regular expressions to describe patterns that we want to match (e.g. Excel/ Sheets, grep, Perl, python, Java, Ruby).

Under the hood, the first phase of compilers is to transform the strings we write in code to tokens (keywords, operators, identifiers, literals). Compilers use regular expressions to describe the sets of strings that can be used for each token type.

Next time: we’ll start to see how to build machines that decide whether strings match the pattern described by a regular expression.

Extra examples for practice:

Which regular expression(s) below describe a language that includes the string $a$ as an element?

$a^* b^*$

$a(ba)^* b$

$a^* \cup b^*$

$(aaa)^*$

$(\varepsilon \cup a) b$

Week1 friday

Review: Determine whether each statement below about regular expressions over the alphabet $\{a,b,c\}$ is true or false:

True or False: $a \in L(~(a \cup b )~\cup c)$

True or False: $ab \in L(~ (a \cup b)^* ~)$

True or False: $ba \in L( ~ a^* b^* ~)$

True or False: $\varepsilon \in L(a \cup b \cup c)$

True or False: $\varepsilon \in L(~ (a \cup b)^* ~)$

True or False: $\varepsilon \in L( ~ a^* b^* ~)$

From the pre-class reading, pages 34-36: A deterministic finite automaton (DFA) is specified by $M = (Q, \Sigma, \delta, q_0, F)$. This $5$-tuple is called the formal definition of the DFA. The DFA can also be represented by its state diagram: with nodes for the state, labelled edges specifying the transition function, and decorations on nodes denoting the start and accept states.

Finite set of states $Q$ can be labelled by any collection of distinct names. Often we use default state labels $q0, q1, \ldots$

The alphabet $\Sigma$ determines the possible inputs to the automaton. Each input to the automaton is a string over $\Sigma$, and the automaton “processes” the input one symbol (or character) at a time.

The transition function $\delta$ gives the next state of the DFA based on the current state of the machine and on the next input symbol.

The start state $q_0$ is an element of $Q$. Each computation of the machine starts at the start state.

The accept (final) states $F$ form a subset of the states of the DFA, $F \subseteq Q$. These states are used to flag if the machine accepts or rejects an input string.

The computation of a machine on an input string is a sequence of states in the machine, starting with the start state, determined by transitions of the machine as it reads successive input symbols.

The DFA $M$ accepts the given input string exactly when the computation of $M$ on the input string ends in an accept state. $M$ rejects the given input string exactly when the computation of $M$ on the input string ends in a nonaccept state, that is, a state that is not in $F$.

The language of $M$, $L(M)$, is defined as the set of all strings that are each accepted by the machine $M$. Each string that is rejected by $M$ is not in $L(M)$. The language of $M$ is also called the language recognized by $M$.

What is finite about all deterministic finite automata? (Select all that apply)

The size of the machine (number of states, number of arrows)
The number of strings that are accepted by the machine
The length of each computation of the machine

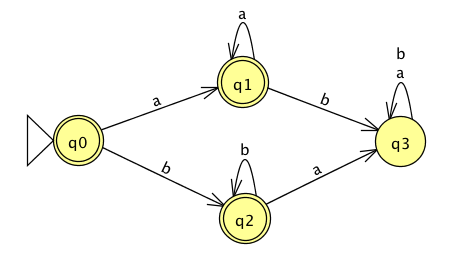
The formal definition of this DFA is

Classify each string $a, aa, ab, ba, bb, \varepsilon$ as accepted by the DFA or rejected by the DFA.

Why are these the only two options?

The language recognized by this DFA is

The language recognized by this DFA is

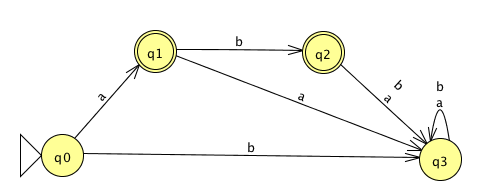
The language recognized by this DFA is

\(\delta\)	\(a\)	\(b\)
\(q\)	\(r\)	\(q\)
\(r\)	\(r\)	\(s\)
\(s\)	\(s\)	\(s\)

Assuming \(\Sigma\) is the alphabet, we use the following conventions
\(\Sigma\)	regular expression describing language consisting of all strings of length \(1\) over \(\Sigma\)
\(*\) then \(\circ\) then \(\cup\)	precedence order, unless parentheses are used to change it
\(R_1R_2\)	shorthand for \(R_1 \circ R_2\) (concatenation symbol is implicit)
\(R^+\)	shorthand for \(R^* \circ R\)
\(R^k\)	shorthand for \(R\) concatenated with itself \(k\) times, where \(k\) is a natural number
Pages 63 - 65