\(M_1\)
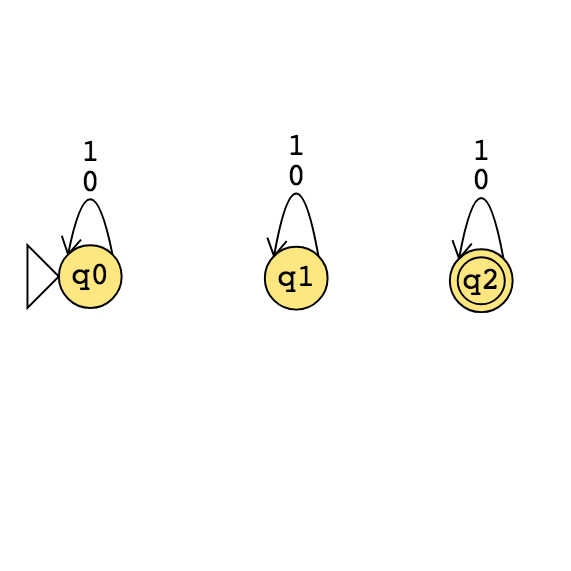 |
\(M_2\)
 |
\(M_3\)
 |
| Suppose \(M\) is a TM | Suppose \(D\) is a TM | Suppose \(E\) is an enumerator | |
| that recognizes \(L\) | that decides \(L\) | that enumerates \(L\) | |
| If string \(w\) is in \(L\) then … | |||
| If string \(w\) is not in \(L\) then … | |||
Describing Turing machines (Sipser p. 185)
The Church-Turing thesis posits that each algorithm can be implemented by some Turing machine
High-level descriptions of Turing machine algorithms are written as indented text within quotation marks.
Stages of the algorithm are typically numbered consecutively.
The first line specifies the input to the machine, which must be a string. This string may be the encoding of some object or list of objects.
Notation: \(\langle O \rangle\) is the string that encodes the object \(O\). \(\langle O_1, \ldots, O_n \rangle\) is the string that encodes the list of objects \(O_1, \ldots, O_n\).
Assumption: There are Turing machines that can be called as subroutines to decode the string representations of common objects and interact with these objects as intended (data structures).
For example, since there are algorithms to answer each of the following questions, by Church-Turing thesis, there is a Turing machine that accepts exactly those strings for which the answer to the question is “yes”
Does a string over \(\{0,1\}\) have even length?
Does a string over \(\{0,1\}\) encode a string of ASCII characters?1
Does a DFA have a specific number of states?
Do two NFAs have any state names in common?
Do two CFGs have the same start variable?
A computational problem is decidable iff language encoding its positive problem instances is decidable.
The computational problem “Does a specific DFA accept a given string?” is encoded by the language \[\begin{aligned} &\{ \textrm{representations of DFAs $M$ and strings $w$ such that $w \in L(M)$}\} \\ =& \{ \langle M, w \rangle \mid M \textrm{ is a DFA}, w \textrm{ is a string}, w \in L(M) \} \end{aligned}\]
The computational problem “Is the language generated by a CFG empty?” is encoded by the language \[\begin{aligned} &\{ \textrm{representations of CFGs $G$ such that $L(G) = \emptyset$}\} \\ =& \{ \langle G \rangle \mid G \textrm{ is a CFG}, L(G) = \emptyset \} \end{aligned}\]
The computational problem “Is the given Turing machine a decider?” is encoded by the language \[\begin{aligned} &\{ \textrm{representations of TMs $M$ such that $M$ halts on every input}\} \\ =& \{ \langle M \rangle \mid M \textrm{ is a TM and for each string } w, \textrm{$M$ halts on $w$} \} \end{aligned}\]
Note: writing down the language encoding a computational problem is only the first step in determining if it’s recognizable, decidable, or …
Some classes of computational problems help us understand the differences between the machine models we’ve been studying:
| Acceptance problem | ||
| …for DFA | \(A_{DFA}\) | \(\{ \langle B,w \rangle \mid \text{$B$ is a DFA that accepts input string $w$}\}\) |
| …for NFA | \(A_{NFA}\) | \(\{ \langle B,w \rangle \mid \text{$B$ is a NFA that accepts input string $w$}\}\) |
| …for regular expressions | \(A_{REX}\) | \(\{ \langle R,w \rangle \mid \text{$R$ is a regular expression that generates input string $w$}\}\) |
| …for CFG | \(A_{CFG}\) | \(\{ \langle G,w \rangle \mid \text{$G$ is a context-free grammar that generates input string $w$}\}\) |
| …for PDA | \(A_{PDA}\) | \(\{ \langle B,w \rangle \mid \text{$B$ is a PDA that accepts input string $w$}\}\) |
| Language emptiness testing | ||
| …for DFA | \(E_{DFA}\) | \(\{ \langle A \rangle \mid \text{$A$ is a DFA and $L(A) = \emptyset$\}}\) |
| …for NFA | \(E_{NFA}\) | \(\{ \langle A\rangle \mid \text{$A$ is a NFA and $L(A) = \emptyset$\}}\) |
| …for regular expressions | \(E_{REX}\) | \(\{ \langle R \rangle \mid \text{$R$ is a regular expression and $L(R) = \emptyset$\}}\) |
| …for CFG | \(E_{CFG}\) | \(\{ \langle G \rangle \mid \text{$G$ is a context-free grammar and $L(G) = \emptyset$\}}\) |
| …for PDA | \(E_{PDA}\) | \(\{ \langle A \rangle \mid \text{$A$ is a PDA and $L(A) = \emptyset$\}}\) |
| Language equality testing | ||
| …for DFA | \(EQ_{DFA}\) | \(\{ \langle A, B \rangle \mid \text{$A$ and $B$ are DFAs and $L(A) =L(B)$\}}\) |
| …for NFA | \(EQ_{NFA}\) | \(\{ \langle A, B \rangle \mid \text{$A$ and $B$ are NFAs and $L(A) =L(B)$\}}\) |
| …for regular expressions | \(EQ_{REX}\) | \(\{ \langle R, R' \rangle \mid \text{$R$ and $R'$ are regular expressions and $L(R) =L(R')$\}}\) |
| …for CFG | \(EQ_{CFG}\) | \(\{ \langle G, G' \rangle \mid \text{$G$ and $G'$ are CFGs and $L(G) =L(G')$\}}\) |
| …for PDA | \(EQ_{PDA}\) | \(\{ \langle A, B \rangle \mid \text{$A$ and $B$ are PDAs and $L(A) =L(B)$\}}\) |
| Sipser Section 4.1 | ||
\(M_1\)
 |
\(M_2\)
 |
\(M_3\)
 |
Example strings in \(A_{DFA}\)
Example strings in \(E_{DFA}\)
Example strings in \(EQ_{DFA}\)
Food for thought: which of the following computational problems are decidable: \(A_{DFA}\)?, \(E_{DFA}\)?, \(EQ_{DFA}\)?
Deciding a computational problem means building / defining a Turing machine that recognizes the language encoding the computational problem, and that is a decider.
| Acceptance problem | ||
| for … | \(A_{\ldots}\) | \(\{ \langle B,w \rangle \mid \text{$B$ is a \ldots that accepts input string $w$}\}\) |
| Language emptiness testing | ||
| for … | \(E_{\ldots}\) | \(\{ \langle A \rangle \mid \text{$A$ is a \ldots and $L(A) = \emptyset$\}}\) |
| Language equality testing | ||
| for … | \(EQ_{\ldots}\) | \(\{ \langle A, B \rangle \mid \text{$A$ and $B$ are \ldots and $L(A) =L(B)$\}}\) |
| Sipser Section 4.1 | ||
\(M_1 =\) “On input \(\langle M,w\rangle\), where \(M\) is a DFA and \(w\) is a string:
Type check encoding to check input is correct type.
Simulate \(M\) on input \(w\) (by keeping track of states in \(M\), transition function of \(M\), etc.)
If the simulations ends in an accept state of \(M\), accept. If it ends in a non-accept state of \(M\), reject. "
What is \(L(M_1)\)?
Is \(L(M_1)\) a decider?
\(M_2 =\)“On input \(\langle M, w \rangle\) where \(M\) is a DFA and \(w\) is a string,
Run \(M\) on input \(w\).
If \(M\) accepts, accept; if \(M\) rejects, reject."
What is \(L(M_2)\)?
Is \(M_2\) a decider?
\(A_{REX} =\)
\(A_{NFA} =\)
True / False: \(A_{REX} = A_{NFA} = A_{DFA}\)
True / False: \(A_{REX} \cap A_{NFA} = \emptyset\), \(A_{REX} \cap A_{DFA} = \emptyset\), \(A_{DFA} \cap A_{NFA} = \emptyset\)
A Turing machine that decides \(A_{NFA}\) is:
A Turing machine that decides \(A_{REX}\) is:
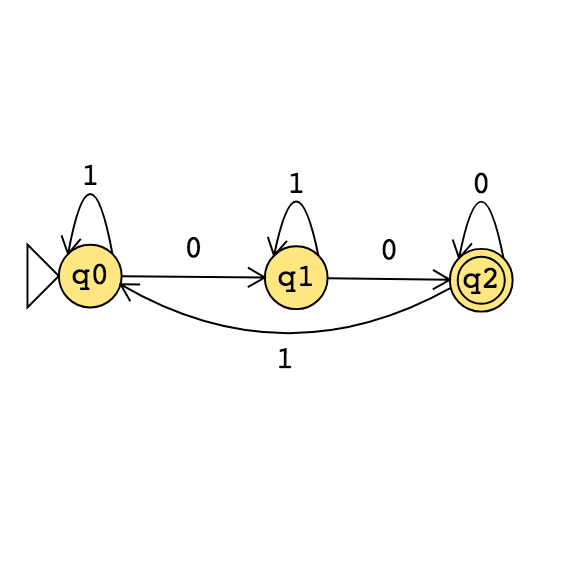
\(M_3 =\)“On input \(\langle M\rangle\) where \(M\) is a DFA,
For integer \(i = 1, 2, \ldots\)
Let \(s_i\) be the \(i\)th string over the alphabet of \(M\) (ordered in string order).
Run \(M\) on input \(s_i\).
If \(M\) accepts, \(\underline{\phantom{FILL IN BLANK}}\). If \(M\) rejects, increment \(i\) and keep going."
Choose the correct option to help fill in the blank so that \(M_3\) recognizes \(E_{DFA}\)
accepts
rejects
loop for ever
We can’t fill in the blank in any way to make this work
None of the above
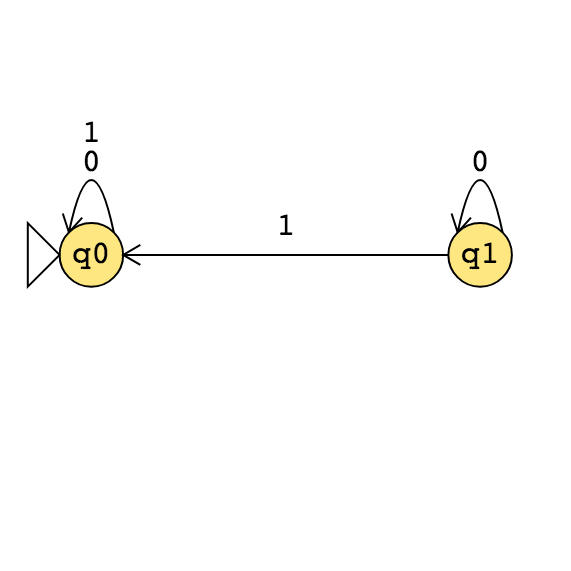
\(M_4 =\) “ On input \(\langle M \rangle\) where \(M\) is a DFA,
Mark the start state of \(M\).
Repeat until no new states get marked:
Loop over the states of \(M\).
Mark any unmarked state that has an incoming edge from a marked state.
If no accept state of \(A\) is marked, \(\underline{\phantom{FILL IN BLANK}}\); otherwise, \(\underline{\phantom{FILL IN BLANK}}\)".
To build a Turing machine that decides \(EQ_{DFA}\), notice that \[L_1 = L_2 \qquad\textrm{iff}\qquad (~(L_1 \cap \overline{L_2}) \cup (L_2 \cap \overline L_1)~) = \emptyset\] There are no elements that are in one set and not the other
\(M_{EQDFA} =\)
Summary: We can use the decision procedures (Turing machines) of decidable problems as subroutines in other algorithms. For example, we have subroutines for deciding each of \(A_{DFA}\), \(E_{DFA}\), \(EQ_{DFA}\). We can also use algorithms for known constructions as subroutines in other algorithms. For example, we have subroutines for: counting the number of states in a state diagram, counting the number of characters in an alphabet, converting DFA to a DFA recognizing the complement of the original language or a DFA recognizing the Kleene star of the original language, constructing a DFA or NFA from two DFA or NFA so that we have a machine recognizing the language of the union (or intersection, concatenation) of the languages of the original machines; converting regular expressions to equivalent DFA; converting DFA to equivalent regular expressions, etc.
| Acceptance problem | ||
| …for DFA | \(A_{DFA}\) | \(\{ \langle B,w \rangle \mid \text{$B$ is a DFA that accepts input string $w$}\}\) |
| …for NFA | \(A_{NFA}\) | \(\{ \langle B,w \rangle \mid \text{$B$ is a NFA that accepts input string $w$}\}\) |
| …for regular expressions | \(A_{REX}\) | \(\{ \langle R,w \rangle \mid \text{$R$ is a regular expression that generates input string $w$}\}\) |
| …for CFG | \(A_{CFG}\) | \(\{ \langle G,w \rangle \mid \text{$G$ is a context-free grammar that generates input string $w$}\}\) |
| …for PDA | \(A_{PDA}\) | \(\{ \langle B,w \rangle \mid \text{$B$ is a PDA that accepts input string $w$}\}\) |
| Acceptance problem | ||
| for Turing machines | \(A_{TM}\) | \(\{ \langle M,w \rangle \mid \text{$M$ is a Turing machine that accepts input string $w$}\}\) |
| Language emptiness testing | ||
| for Turing machines | \(E_{TM}\) | \(\{ \langle M \rangle \mid \text{$M$ is a Turing machine and $L(M) = \emptyset$\}}\) |
| Language equality testing | ||
| for Turing machines | \(EQ_{TM}\) | \(\{ \langle M_1, M_2 \rangle \mid \text{$M_1$ and $M_2$ are Turing machines and $L(M_1) =L(M_2)$\}}\) |
| Sipser Section 4.1 | ||
3 \(M_1\) 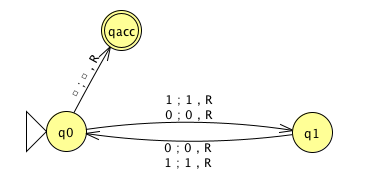
\(M_2\) 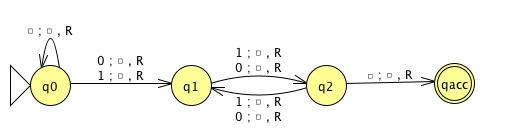
\(M_3\) 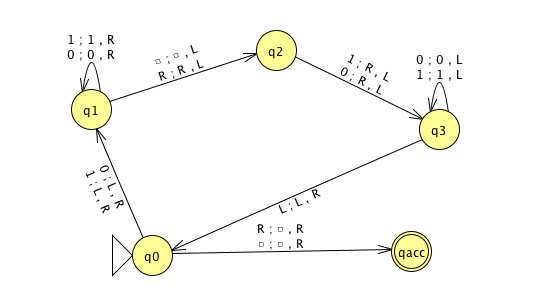
Example strings in \(A_{TM}\)
Example strings in \(E_{TM}\)
Example strings in \(EQ_{TM}\)
Theorem: \(A_{TM}\) is Turing-recognizable.
Strategy: To prove this theorem, we need to define a Turing machine \(R_{ATM}\) such that \(L(R_{ATM}) = A_{TM}\).
Define \(R_{ATM} =\) “
Proof of correctness:
We will show that \(A_{TM}\) is undecidable. First, let’s explore what that means.
A Turing-recognizable language is a set of strings that is the language recognized by some Turing machine. We also say that such languages are recognizable.
A Turing-decidable language is a set of strings that is the language recognized by some decider. We also say that such languages are decidable.
An unrecognizable language is a language that is not Turing-recognizable.
An undecidable language is a language that is not Turing-decidable.
True or False: Any undecidable language is also unrecognizable.
True or False: Any unrecognizable language is also undecidable.
To prove that a computational problem is decidable, we find/ build a Turing machine that recognizes the language encoding the computational problem, and that is a decider.
How do we prove a specific problem is not decidable?
How would we even find such a computational problem?
Counting arguments for the existence of an undecidable language:
The set of all Turing machines is countably infinite.
Each Turing-recognizable language is associated with a Turing machine in a one-to-one relationship, so there can be no more Turing-recognizable languages than there are Turing machines.
Since there are infinitely many Turing-recognizable languages (think of the singleton sets), there are countably infinitely many Turing-recognizable languages.
Such the set of Turing-decidable languages is an infinite subset of the set of Turing-recognizable languages, the set of Turing-decidable languages is also countably infinite.
Since there are uncountably many languages (because \(\mathcal{P}(\Sigma^*)\) is uncountable), there are uncountably many unrecognizable languages and there are uncountably many undecidable languages.
Thus, there’s at least one undecidable language!
What’s a specific example of a language that is unrecognizable or undecidable?
To prove that a language is undecidable, we need to prove that there is no Turing machine that decides it.
Key idea: proof by contradiction relying on self-referential disagreement.
We will use vocabulary that should be familiar from your discrete math and introduction to proofs classes. Some of the notation conventions may be a bit different: we will use the notation from this class’ textbook2.
Write out in words the meaning of the symbols below: \[\{ a,b, c\}\]
\[| \{a, b, a \} | = 2\]
\[| aba | = 3\]
\[(a, 3, 2, b, b)\]
| Term | Typical symbol | Meaning |
|---|---|---|
| Alphabet | \(\Sigma\), \(\Gamma\) | A non-empty finite set |
| Symbol over \(\Sigma\) | \(\sigma\), \(b\), \(x\) | An element of the alphabet \(\Sigma\) |
| String over \(\Sigma\) | \(u\), \(v\), \(w\) | A finite list of symbols from \(\Sigma\) |
| The set of all strings over \(\Sigma\) | \(\Sigma^*\) | The collection of all possible strings formed from symbols from \(\Sigma\) |
| (Some) language over \(\Sigma\) | \(L\) | (Some) set of strings over \(\Sigma\) |
| Empty string | \(\varepsilon\) | The string of length \(0\) |
| Empty set | \(\emptyset\) | The empty language |
| Natural numbers | \(\mathcal{N}\) | The set of positive integers |
| Finite set | The empty set or a set whose distinct elements can be counted by a natural number | |
| Infinite set | A set that is not finite. | |
| Pages 3, 4, 13, 14 |
| Term | Notation | Meaning |
|---|---|---|
| Reverse of a string \(w\) | \(w^\mathcal{R}\) | write \(w\) in the opposite order, if \(w = w_1 \cdots w_n\) then \(w^\mathcal{R} = w_n \cdots w_1\). Note: \(\varepsilon^\mathcal{R} = \varepsilon\) |
| Concatenating strings \(x\) and \(y\) | \(xy\) | take \(x = x_1 \cdots x_m\), \(y=y_1 \cdots y_n\) and form \(xy = x_1 \cdots x_m y_1 \cdots y_n\) |
| String \(z\) is a substring of string \(w\) | there are strings \(u,v\) such that \(w = uzv\) | |
| String \(x\) is a prefix of string \(y\) | there is a string \(z\) such that \(y = xz\) | |
| String \(x\) is a proper prefix of string \(y\) | \(x\) is a prefix of \(y\) and \(x \neq y\) | |
| Shortlex order, also known as string order over alphabet \(\Sigma\) | Order strings over \(\Sigma\) first by length and then according to the dictionary order, assuming symbols in \(\Sigma\) have an ordering. | |
| Pages 13, 14 |
Circle the correct choice:
A string over an alphabet \(\Sigma\) is an element of \(\Sigma^*\) OR a subset of \(\Sigma^*\).
A language over an alphabet \(\Sigma\) is an element of \(\Sigma^*\) OR a subset of \(\Sigma^*\).
Extra examples for practice:
With \(\Sigma_1 = \{0,1\}\) and \(\Sigma_2 = \{a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z\}\) and \(\Gamma = \{0,1,x,y,z\}\)
An example of a string of length 3 over \(\Sigma_1\) is
An example of a string of length 1 over \(\Sigma_2\) is
The number of distinct strings of length 2 over \(\Gamma\) is
An example of a language over \(\Sigma_1\) of size \(1\) is
An example of an infinite language over \(\Sigma_1\) is
An example of a finite language over \(\Gamma\) is
True or False: \(\varepsilon \in \Sigma_1\)
True or False: \(\varepsilon\) is a string over \(\Sigma_1\)
True or False: \(\varepsilon\) is a language over \(\Sigma_1\)
True or False: \(\varepsilon\) is a prefix of some string over \(\Sigma_1\)
True or False: There is a string over \(\Sigma_1\) that is a proper prefix of \(\varepsilon\)
The first five strings over \(\Sigma_1\) in string order, using the ordering \(0 < 1\):
The first five strings over \(\Sigma_2\) in string order, using the usual alphabetical ordering for single letters:
An introduction to ASCII is available on the w3 tutorial here.↩︎
Page references are to the 3rd edition (International) of Siper’s Introduction to the Theory of Computation, available at the campus bookstore for under $20. Copies of the book are also available for those who can’t access the book to borrow from the course instructor, while supplies last (minnes@eng.ucsd.edu)↩︎