Monday May 2
For Turing machine \(M= (Q, \Sigma, \Gamma,
\delta, q_0, q_{accept}, q_{reject})\) the
computation of \(M\) on a string \(w\) over \(\Sigma\) is:
Read/write head starts at leftmost position on tape.
Input string is written on \(|w|\)-many leftmost cells of tape, rest of
the tape cells have the blank symbol. Tape
alphabet is \(\Gamma\)
with \(\textvisiblespace\in \Gamma\)
and \(\Sigma \subseteq \Gamma\). The
blank symbol \(\textvisiblespace \notin
\Sigma\).
Given current state of machine and current symbol being read at
the tape head, the machine transitions to next state, writes a symbol to
the current position of the tape head (overwriting existing symbol), and
moves the tape head L or R (if possible). Formally,
transition function is \[\delta: Q\times \Gamma \to Q \times \Gamma \times
\{L, R\}\]
Computation ends if and when machine enters either the accept or
the reject state. This is called halting.
Note: \(q_{accept} \neq
q_{reject}\).
The language recognized by the Turing
machine \(M\), is \[\{ w \in \Sigma^* \mid \textrm{computation of $M$
on $w$ halts after entering the accept state}\} = \{ w \in \Sigma^* \mid
w \textrm{ is accepted by } M\}\]
To define a Turing machine, we could give a
Formal definition, namely the \(7\)-tuple of parameters including set of
states, input alphabet, tape alphabet, transition function, start state,
accept state, and reject state; or,
Implementation-level definition:
English prose that describes the Turing machine head movements relative
to contents of tape, and conditions for accepting / rejecting based on
those contents.
Conventions for drawing state diagrams of Turing machines: (1) omit
the reject state from the diagram (unless it’s the start state), (2) any
missing transitions in the state diagram have value \((q_{reject}, ~\textvisiblespace~ ,
R)\).
Sipser Figure 3.10
2
Implementation level description of this machine:
Zig-zag across tape to corresponding positions on either side of
\(\#\) to check whether the characters
in these positions agree. If they do not, or if there is no \(\#\), reject. If they do, cross them
off.
Once all symbols to the left of the \(\#\) are crossed off, check for any
un-crossed-off symbols to the right of \(\#\); if there are any, reject; if there
aren’t, accept.
Computation on input string \(01\#01\)
| \(0\) |
\(1\) |
\(\#\) |
\(0\) |
\(1\) |
\(\textvisiblespace\) |
\(\textvisiblespace\) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
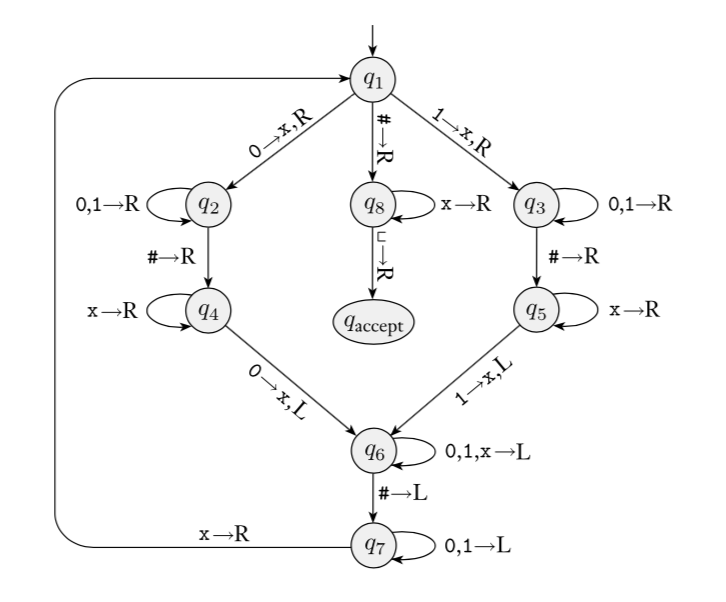
The language recognized by this machine is \[\{ w \# w \mid w \in \{0,1\}^* \}\]
A language \(L\) is
recognized by a Turing machine \(M\) means
A Turing machine \(M\)
recognizes a language \(L\) if means
A Turing machine \(M\) is a
decider means
A language \(L\) is
decided by a Turing machine \(M\) means
A Turing machine \(M\)
decides a language \(L\) means
Fix \(\Sigma = \{0,1\}\), \(\Gamma = \{ 0, 1, \textvisiblespace\}\) for
the Turing machines with the following state diagrams:
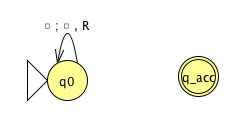 |
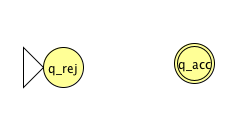 |
| Implementation level description: |
Implementation level description: |
|
|
|
|
|
|
| Example of string accepted: |
Example of string accepted: |
| Example of string rejected: |
Example of string rejected: |
|
|
| Decider? Yes / No |
Decider? Yes / No |
|
|
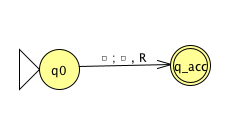 |
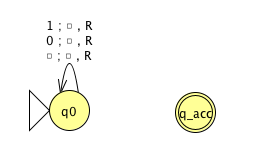 |
| Implementation level description: |
Implementation level description: |
|
|
|
|
|
|
| Example of string accepted: |
Example of string accepted: |
| Example of string rejected: |
Example of string rejected: |
|
|
| Decider? Yes / No |
Decider? Yes / No |
|
|
Review: Week 6
Monday
Recall: Review quizzes based on class material are assigned each day.
These quizzes will help you track and confirm your understanding of the
concepts and examples we work in class. Quizzes can be submitted on
Gradescope as many times (with no penalty) as you like until the quiz
deadline: the three quizzes each week are all due on Friday (with no
penalty late submission open until Sunday).
Please complete the review quiz questions on Gradescope about formal and
implementation-level descriptions of Turing machines.
Pre class reading for next time: pages
176-177 on variants of Turing machines
Wednesday May 4
Two models of computation are called equally
expressive when every language recognizable with the
first model is recognizable with the second, and vice versa.
True / False: NFAs and PDAs are equally expressive.
True / False: Regular expressions and CFGs are equally
expressive.
Some examples of models that are equally
expressive with deterministic Turing machines:
The May-stay machine model is the same as the usual Turing machine
model, except that on each transition, the tape head may move L, move R,
or Stay.
Formally: \((Q, \Sigma, \Gamma, \delta,
q_0, q_{accept}, q_{reject})\) where \[\delta: Q \times \Gamma \to Q \times \Gamma
\times \{L, R, S\}\]
Claim: Turing machines and May-stay
machines are equally expressive. To prove …
To translate a standard TM to a may-stay machine:
To translate one of the may-stay machines to standard TM: any time TM
would Stay, move right then left.
Formally: suppose \(M_S = (Q, \Sigma,
\Gamma, \delta, q_0, q_{acc}, q_{rej})\) has \(\delta: Q \times \Gamma \to Q \times \Gamma \times
\{L, R, S\}\). Define the Turing-machine \[M_{new}
= (\phantom{\hspace{2.5in}})\]
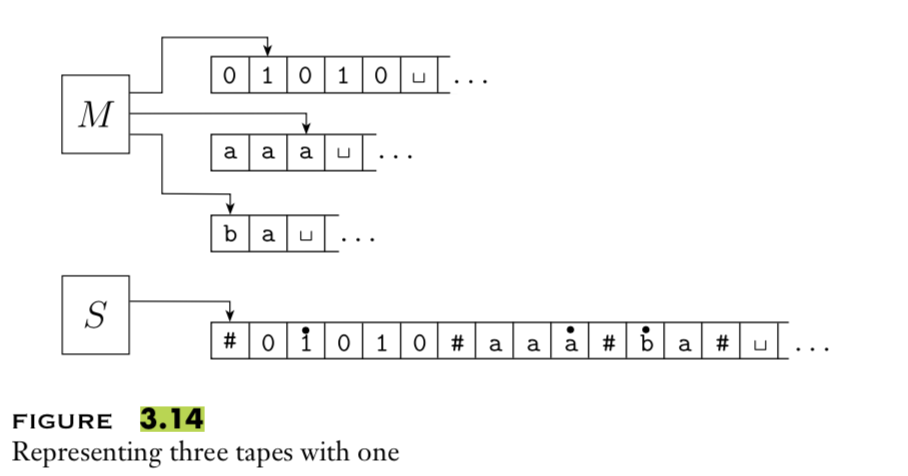
A multitape Turing macihne with \(k\) tapes can be formally representated as
\((Q, \Sigma, \Gamma, \delta, q_0, q_{acc},
q_{rej})\) where \(Q\) is the
finite set of states, \(\Sigma\) is the
input alphabet with \(\textvisiblespace \notin
\Sigma\), \(\Gamma\) is the tape
alphabet with \(\Sigma \subsetneq
\Gamma\) , \(\delta: Q\times
\Gamma^k\to Q \times \Gamma^k \times \{L,R\}^k\) (where \(k\) is the number of states)
If \(M\) is a standard TM, it is a
\(1\)-tape machine.
To translate a \(k\)-tape machine to
a standard TM: Use a new symbol to separate the contents of each tape
and keep track of location of head with special version of each tape
symbol. Sipser Theorem 3.13
Extra practice: Define a machine \((Q, \Gamma, b, \Sigma, q_0, F, \delta)\)
where \(Q\) is the finite set of states
\(\Gamma\) is the tape alphabet, \(b \in \Gamma\) is the blank symbol, \(\Sigma \subsetneq \Gamma\) is the input
alphabet, \(q_0 \in Q\) is the start
state, \(F \subseteq Q\) is the set of
accept states, \(\delta: (Q \setminus
F) \times \Gamma \not\to Q \times \Gamma \times \{L, R\}\) is
a partial transition function If computation enters a state in \(F\), it accepts If computation enters a
configuration where \(\delta\) is not
defined, it rejects . Hopcroft and Ullman, cited by
Wikipedia
Enumerators give a different model of computation where a language is
produced, one string at a time, rather
than recognized by accepting (or not) individual strings.
Each enumerator machine has finite state control, unlimited work
tape, and a printer. The computation proceeds according to transition
function; at any point machine may “send” a string to the printer. \[E = (Q, \Sigma, \Gamma, \delta, q_0,
q_{print})\] \(Q\) is the finite
set of states, \(\Sigma\) is the output
alphabet, \(\Gamma\) is the tape
alphabet (\(\Sigma \subsetneq\Gamma,
\textvisiblespace \in \Gamma \setminus \Sigma\)), \[\delta: Q \times \Gamma \times \Gamma \to Q
\times \Gamma \times \Gamma \times \{L, R\} \times \{L, R\}\]
where in state \(q\), when the working
tape is scanning character \(x\) and
the printer tape is scanning character \(y\), \(\delta(
(q,x,y) ) = (q', x', y', d_w, d_p)\) means transition
to control state \(q'\), write
\(x'\) on the working tape, write
\(y'\) on the printer tape, move in
direction \(d_w\) on the working tape,
and move in direction \(d_p\) on the
printer tape. The computation starts in \(q_0\) and each time the computation enters
\(q_{print}\) the string from the
leftmost edge of the printer tape to the first blank cell is considered
to be printed.
The language enumerated by \(E\), \(L(E)\), is \(\{ w
\in \Sigma^* \mid \text{$E$ eventually, at finite time,
prints $w$} \}\).
cc  &
&
| \(\textvisiblespace ~*\) |
\(\textvisiblespace\) |
\(\textvisiblespace\) |
\(\textvisiblespace\) |
\(\textvisiblespace\) |
\(\textvisiblespace\) |
\(\textvisiblespace\) |
| \(\textvisiblespace ~*\) |
\(\textvisiblespace\) |
\(\textvisiblespace\) |
\(\textvisiblespace\) |
\(\textvisiblespace\) |
\(\textvisiblespace\) |
\(\textvisiblespace\) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Theorem 3.21 A language is
Turing-recognizable iff some enumerator enumerates it. Proof
next time …
Review: Week 6
Wednesday
Please complete the review quiz questions on Gradescope about variants of Turing
machines.
Pre class reading for next time:
Theorem 3.16 on page 178 (nondeterministism)
Friday May 6
To define a Turing machine, we could give a
Formal definition: the \(7\)-tuple of parameters including set of
states, input alphabet, tape alphabet, transition function, start state,
accept state, and reject state; or,
Implementation-level definition:
English prose that describes the Turing machine head movements relative
to contents of tape, and conditions for accepting / rejecting based on
those contents.
High-level description: description
of algorithm (precise sequence of instructions), without implementation
details of machine. As part of this description, can “call" and run
another TM as a subroutine.
Theorem 3.21 A language is
Turing-recognizable iff some enumerator enumerates it.
Proof:
Assume \(L\) is enumerated by some
enumerator, \(E\), so \(L = L(E)\). We’ll use \(E\) in a subroutine within a high-level
description of a new Turing machine that we will build to recognize
\(L\).
Goal: build Turing machine \(M_E\) with \(L(M_E) = L(E)\).
Define \(M_E\) as follows: \(M_E =\) “On input \(w\),
Run \(E\). For each string \(x\) printed by \(E\).
Check if \(x = w\). If so,
accept (and halt); otherwise, continue."
Assume \(L\) is Turing-recognizable
and there is a Turing machine \(M\)
with \(L = L(M)\). We’ll use \(M\) in a subroutine within a high-level
description of an enumerator that we will build to enumerate \(L\).
Goal: build enumerator \(E_M\) with \(L(E_M) = L(M)\).
Idea: check each string in turn to see
if it is in \(L\).
How? Run computation of \(M\) on each string.
But: need to be careful about computations that
don’t halt.
Recall String order for \(\Sigma = \{0,1\}\): \(s_1 = \varepsilon\), \(s_2 = 0\), \(s_3
= 1\), \(s_4 = 00\), \(s_5 = 01\), \(s_6 = 10\), \(s_7 = 11\), \(s_8 = 000\), …
Define \(E_M\) as follows: \(E_{M} =\) “ ignore any
input. Repeat the following for \(i=1, 2, 3, \ldots\)
Run the computations of \(M\) on
\(s_1\), \(s_2\), …, \(s_i\) for (at most) \(i\) steps each
For each of these \(i\)
computations that accept during the (at most) \(i\) steps, print out the accepted
string."
Nondeterministic Turing machine
At any point in the computation, the nondeterministic machine may
proceed according to several possibilities: \((Q, \Sigma, \Gamma, \delta, q_0, q_{acc},
q_{rej})\) where \[\delta: Q \times
\Gamma \to \mathcal{P}(Q \times \Gamma \times \{L, R\})\] The
computation of a nondeterministic Turing machine is a tree with
branching when the next step of the computation has multiple
possibilities. A nondeterministic Turing machine accepts a string
exactly when some branch of the computation tree enters the accept
state.
Given a nondeterministic machine, we can use a \(3\)-tape Turing machine to simulate it by
doing a breadth-first search of computation tree: one tape is
“read-only” input tape, one tape simulates the tape of the
nondeterministic computation, and one tape tracks nondeterministic
branching. Sipser page 178
Two models of computation are called equally
expressive when every language recognizable with the
first model is recognizable with the second, and vice versa.
Church-Turing Thesis (Sipser p. 183):
The informal notion of algorithm is formalized completely and correctly
by the formal definition of a Turing machine. In other words: all
reasonably expressive models of computation are equally expressive with
the standard Turing machine.
Claim: If two languages (over a fixed
alphabet \(\Sigma\)) are
Turing-recognizable, then their union is as well.
Proof using Turing machines:
Proof using nondeterministic Turing
machines:
Proof using enumerators:
Review: Week 6
Friday
Please complete the review quiz questions on Gradescope about descriptions of Turing
machines.
Pre class reading for next time: Page
184-185 Terminology for describing Turing machines




 &
&