Recap so far: In DFA, the only memory available is in the states. Automata can only “remember” finitely far in the past and finitely much information, because they can have only finitely many states. If a computation path of a DFA visits the same state more than once, the machine can’t tell the difference between the first time and future times it visits this state. Thus, if a DFA accepts one long string, then it must accept (infinitely) many similar strings.
Definition A positive integer \(p\) is a pumping length of a language \(L\) over \(\Sigma\) means that, for each string \(s \in \Sigma^*\), if \(|s| \geq p\) and \(s \in L\), then there are strings \(x,y,z\) such that \[s = xyz\] and \[|y| > 0, \qquad \qquad \text{ for each $i \geq 0$, $xy^i z \in L$}, \qquad \text{and} \qquad \qquad |xy| \leq p.\]
Negation: A positive integer \(p\) is not a pumping length of a language \(L\) over \(\Sigma\) iff \[\exists s \left(~ |s| \geq p \wedge s \in L \wedge \forall x \forall y \forall z \left( ~\left( s = xyz \wedge |y| > 0 \wedge |xy| \leq p~ \right) \to \exists i ( i \geq 0 \wedge xy^iz \notin L ) \right) ~\right)\] Informally:
Restating Pumping Lemma: If \(L\) is a regular language, then it has a pumping length.
Contrapositive: If \(L\) has no pumping length, then it is nonregular.
The Pumping Lemma cannot be used to prove that a language is regular.
The Pumping Lemma can be used to prove that a language is not regular.
Extra practice: Exercise 1.49 in the book.
Proof strategy: To prove that a language \(L\) is not regular,
Consider an arbitrary positive integer \(p\)
Prove that \(p\) is not a pumping length for \(L\)
Conclude that \(L\) does not have any pumping length, and therefore it is not regular.
Example: \(\Sigma = \{0,1\}\), \(L = \{ 0^n 1^n \mid n \geq 0\}\).
Fix \(p\) an arbitrary positive integer. List strings that are in \(L\) and have length greater than or equal to \(p\):
Pick \(s =\)
Suppose \(s = xyz\) with \(|xy| \leq p\) and \(|y| > 0\).
Then when \(i = \hspace{1in}\), \(xy^i z = \hspace{1in}\)
Example: \(\Sigma = \{0,1\}\), \(L = \{w w^{\mathcal{R}} \mid w \in \{0,1\}^*\}\).
Fix \(p\) an arbitrary positive integer. List strings that are in \(L\) and have length greater than or equal to \(p\):
Pick \(s =\)
Suppose \(s = xyz\) with \(|xy| \leq p\) and \(|y| > 0\).
Then when \(i = \hspace{1in}\), \(xy^i z = \hspace{1in}\)
Example: \(\Sigma = \{0,1\}\), \(L = \{0^j1^k \mid j \geq k \geq 0\}\).
Fix \(p\) an arbitrary positive integer. List strings that are in \(L\) and have length greater than or equal to \(p\):
Pick \(s =\)
Suppose \(s = xyz\) with \(|xy| \leq p\) and \(|y| > 0\).
Then when \(i = \hspace{1in}\), \(xy^i z = \hspace{1in}\)
Example: \(\Sigma = \{0,1\}\), \(L = \{0^n1^m0^n \mid m,n \geq 0\}\).
Fix \(p\) an arbitrary positive integer. List strings that are in \(L\) and have length greater than or equal to \(p\):
Pick \(s =\)
Suppose \(s = xyz\) with \(|xy| \leq p\) and \(|y| > 0\).
Then when \(i = \hspace{1in}\), \(xy^i z = \hspace{1in}\)
Recall: Review quizzes based on class material are assigned each day. These quizzes will help you track and confirm your understanding of the concepts and examples we work in class. Quizzes can be submitted on Gradescope as many times (with no penalty) as you like until the quiz deadline: the three quizzes each week are all due on Friday (with no penalty late submission open until Sunday).
Please complete the review quiz questions on Gradescope about pumping lemma and nonregular sets.
Pre class reading for next time: Page 112
| Language | \(s \in L\) | \(s \notin L\) | Is the language regular or nonregular? |
|---|---|---|---|
| \(\{a^nb^n \mid 0 \leq n \leq 5 \}\) | |||
| \(\{b^n a^n \mid n \geq 2\}\) | |||
| \(\{a^m b^n \mid 0 \leq m\leq n\}\) | |||
| \(\{a^m b^n \mid m \geq n+3, n \geq 0\}\) | |||
| \(\{b^m a^n \mid m \geq 1, n \geq 3\}\) | |||
| \(\{ w \in \{a,b\}^* \mid w = w^\mathcal{R} \}\) | |||
| \(\{ ww^\mathcal{R} \mid w\in \{a,b\}^* \}\) | |||
Regular sets are not the end of the story
Many nice / simple / important sets are not regular
Limitation of the finite-state automaton model: Can’t "count", Can only remember finitely far into the past, Can’t backtrack, Must make decisions in "real-time"
We know actual computers are more powerful than this model...
The next model of computation. Idea: allow some memory of unbounded size. How?
To generalize regular expressions: context-free
grammars
To generalize NFA: Pushdown automata, which is like an NFA with access to a stack: Number of states is fixed, number of entries in stack is unbounded. At each step (1) Transition to new state based on current state, letter read, and top letter of stack, then (2) (Possibly) push or pop a letter to (or from) top of stack. Accept a string iff there is some sequence of states and some sequence of stack contents which helps the PDA processes the entire input string and ends in an accepting state.

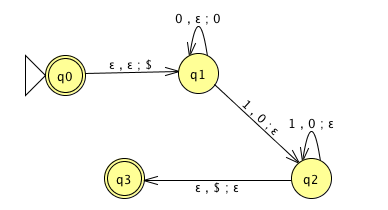
Trace the computation of this PDA on the input string \(01\).
Trace the computation of this PDA on the input string \(011\).
Please complete the review quiz questions on Gradescope about PDA definitions.
Pre class reading for next time: Page 102
Definition A pushdown automaton (PDA) is specified by a \(6\)-tuple \((Q, \Sigma, \Gamma, \delta, q_0, F)\) where \(Q\) is the finite set of states, \(\Sigma\) is the input alphabet, \(\Gamma\) is the stack alphabet, \[\delta: Q \times \Sigma_\varepsilon \times \Gamma_\varepsilon \to \mathcal{P}( Q \times \Gamma_\varepsilon)\] is the transition function, \(q_0 \in Q\) is the start state, \(F \subseteq Q\) is the set of accept states.
2 Formal definition
Draw the state diagram of a PDA with \(\Sigma = \Gamma\).

Draw the state diagram of a PDA with \(\Sigma \cap \Gamma = \emptyset\).
A PDA recognizing the set \(\{ \hspace{1.5 in} \}\) can be informally described as:
Read symbols from the input. As each 0 is read, push it onto the stack. As soon as 1s are seen, pop a 0 off the stack for each 1 read. If the stack becomes empty and there is exactly one 1 left to read, read that 1 and accept the input. If the stack becomes empty and there are either zero or more than one 1s left to read, or if the 1s are finished while the stack still contains 0s, or if any 0s appear in the input following 1s, reject the input.
State diagram for this PDA:
Consider the state diagram of a PDA with input alphabet \(\Sigma\) and stack alphabet \(\Gamma\).
| Label | means |
|---|---|
| \(a, b ; c\) when \(a \in \Sigma\), \(b\in \Gamma\), \(c \in \Gamma\) | |
| \(a, \varepsilon ; c\) when \(a \in \Sigma\), \(c \in \Gamma\) | |
| \(a, b ; \varepsilon\) when \(a \in \Sigma\), \(b\in \Gamma\) | |
| \(a, \varepsilon ; \varepsilon\) when \(a \in \Sigma\) | |
How does the meaning change if \(a\) is replaced by \(\varepsilon\)?
Note: alternate notation is to replace \(;\) with \(\to\)
For the PDA state diagrams below, \(\Sigma = \{0,1\}\).
| Mathematical description of language | State diagram of PDA recognizing language |
|---|---|
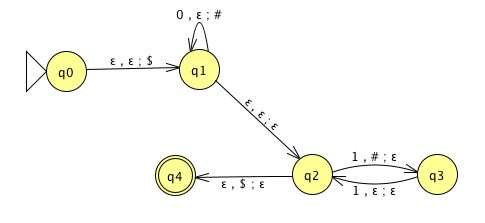 |
|
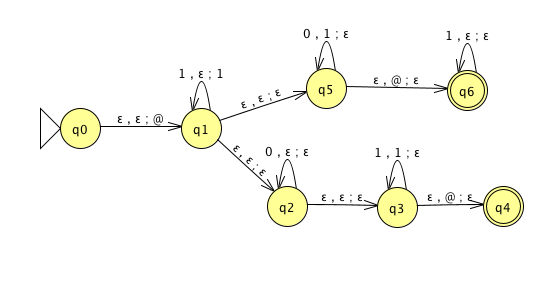 |
|
| \(\{ 0^i 1^j 0^k \mid i,j,k \geq 0 \}\) |
Please complete the review quiz questions on Gradescope about PDA construction.