We are committed to fostering a learning environment for this course that supports a diversity of thoughts, perspectives and experiences, and respects your identities (including race, ethnicity, heritage, gender, sex, class, sexuality, religion, ability, age, educational background, etc.). Our goal is to create a diverse and inclusive learning environment where all students feel comfortable and can thrive.
If you or someone you know is suffering from food and/or housing insecurities there are UCSD resources here to help:
Basic Needs Office: https://basicneeds.ucsd.edu/
Triton Food Pantry (in the old Student Center) is free and anonymous, and includes produce:
https://www.facebook.com/tritonfoodpantry/
Mutual Aid UCSD: https://mutualaiducsd.wordpress.com/
Financial aid resources, the possibility of emergency grant funding, and off-campus housing referral resources are available. See CAPS and your college dean.
If you find yourself in an uncomfortable situation, ask for help. We are committed to upholding University policies regarding nondiscrimination, sexual violence and sexual harassment.
Counseling and Psychological Services (CAPS) at 858 5343755 or http://caps.ucsd.edu
OPHD at (858) 534-8298, ophd@ucsd.edu , http://ophd.ucsd.edu. CARE at Sexual Assault Resource Center at 858 5345793 sarc@ucsd.edu http://care.ucsd.edu
Spring 2022 is still a transition quarter so please be patient with us as we do our best to deliver a great learning opportunity that meets the needs of all students and adheres to the university guidelines.
Please do not come to class if you are sick or even think you might be sick.
Please reach out (minnes@eng.ucsd.edu) if you need support with extenuating circumstances.
Based on current UCSD guidelines (as of March 21), masks are required in class. All students who attend class must also be fully vaccinated against COVID-19 unless they have a university-approved exemption. We will continue to follow the campus guidelines as updated on https://returntolearn.ucsd.edu/ .
Class website: https://cseweb.ucsd.edu/classes/sp22/cse105-a/
Pro-tip: the URL structure is your map to finding your course website for other CSE classes.
Instructor: Prof. Mia Minnes "Minnes" rhymes with Guinness, minnes@eng.ucsd.edu, http://cseweb.ucsd.edu/ minnes
Our team: Six TAs and five tutors + all of you
Fill in contact info for students around you, if you’d like:
On a typical week: MWF Lectures + review quizzes, M Discussion, Th Homework / project due. Office hours and Q+A on Piazza available throughout the week. All dates are on Canvas (click for link) and details are on course calendar (click for link).
Welcome to CSE 105: Introduction to Theory of Computation in Spring 2022!
What problems are computers capable of solving?
What resources are needed to solve a problem?
Are some problems harder than others?
In this context, a problem is defined as: “Making a decision or computing a value based on some input"
Consider the following problems:
Find a file on your computer
Determine if your code will compile
Find a run-time error in your code
Certify that your system is un-hackable
Which of these is hardest?
In Computer Science, we operationalize “hardest” as “requires most resources”, where resources might be memory, time, parallelism, randomness, power, etc.
To be able to compare “hardness” of problems, we use a consistent description of problems
Input: String
Output: Yes/ No, where Yes means that the input string matches the pattern or property described by the problem.
We will use vocabulary that should be familiar from your discrete math and introduction to proofs classes. Some of the notation conventions may be a bit different: we will use the notation from this class’ textbook1.
Write out in words the meaning of the symbols below: \[\{ a,b, c\}\]
\[| \{a, b, a \} | = 2\]
\[| aba | = 3\]
\[(a, 3, 2, b, b)\]
| Term | Typical symbol | Meaning |
|---|---|---|
| Alphabet | \(\Sigma\), \(\Gamma\) | A non-empty finite set |
| Symbol over \(\Sigma\) | \(\sigma\), \(b\), \(x\) | An element of the alphabet \(\Sigma\) |
| String over \(\Sigma\) | \(u\), \(v\), \(w\) | A finite list of symbols from \(\Sigma\) |
| The set of all strings over \(\Sigma\) | \(\Sigma^*\) | The collection of all possible strings formed from symbols from \(\Sigma\) |
| (Some) language over \(\Sigma\) | \(L\) | (Some) set of strings over \(\Sigma\) |
| Empty string | \(\varepsilon\) | The string of length \(0\) |
| Empty set | \(\emptyset\) | The empty language |
| Natural numbers | \(\mathcal{N}\) | The set of positive integers |
| Finite set | The empty set or a set whose distinct elements can be counted by a natural number | |
| Infinite set | A set that is not finite. | |
| Pages 3, 4, 13, 14 |
| Term | Notation | Meaning |
|---|---|---|
| Reverse of a string \(w\) | \(w^\mathcal{R}\) | write \(w\) in the opposite order, if \(w = w_1 \cdots w_n\) then \(w^\mathcal{R} = w_n \cdots w_1\). Note: \(\varepsilon^\mathcal{R} = \varepsilon\) |
| Concatenating strings \(x\) and \(y\) | \(xy\) | take \(x = x_1 \cdots x_m\), \(y=y_1 \cdots y_n\) and form \(xy = x_1 \cdots x_m y_1 \cdots y_n\) |
| String \(z\) is a substring of string \(w\) | there are strings \(u,v\) such that \(w = uzv\) | |
| String \(x\) is a prefix of string \(y\) | there is a string \(z\) such that \(y = xz\) | |
| String \(x\) is a proper prefix of string \(y\) | \(x\) is a prefix of \(y\) and \(x \neq y\) | |
| Shortlex order, also known as string order over alphabet \(\Sigma\) | Order strings over \(\Sigma\) first by length and then according to the dictionary order, assuming symbols in \(\Sigma\) have an ordering. | |
| Pages 13, 14 |
Circle the correct choice:
A string over an alphabet \(\Sigma\) is an element of \(\Sigma^*\) OR a subset of \(\Sigma^*\).
A language over an alphabet \(\Sigma\) is an element of \(\Sigma^*\) OR a subset of \(\Sigma^*\).
Extra examples for practice:
With \(\Sigma_1 = \{0,1\}\) and \(\Sigma_2 = \{a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z\}\) and \(\Gamma = \{0,1,x,y,z\}\)
An example of a string of length 3 over \(\Sigma_1\) is
An example of a string of length 1 over \(\Sigma_2\) is
The number of distinct strings of length 2 over \(\Gamma\) is
An example of a language over \(\Sigma_1\) of size \(1\) is
An example of an infinite language over \(\Sigma_1\) is
An example of a finite language over \(\Gamma\) is
True or False: \(\varepsilon \in \Sigma_1\)
True or False: \(\varepsilon\) is a string over \(\Sigma_1\)
True or False: \(\varepsilon\) is a language over \(\Sigma_1\)
True or False: \(\varepsilon\) is a prefix of some string over \(\Sigma_1\)
True or False: There is a string over \(\Sigma_1\) that is a proper prefix of \(\varepsilon\)
The first five strings over \(\Sigma_1\) in string order, using the ordering \(0 < 1\):
The first five strings over \(\Sigma_2\) in string order, using the usual alphabetical ordering for single letters:
Please complete the beginning of the quarter survey https://forms.gle/9AaEcwwN5EvcJ4qp9
We want you to be familiar with class policies and procedures so you are ready to have a successful quarter. Please take a look at the class website https://cseweb.ucsd.edu/classes/sp22/cse105-a/ and answer the questions about it on Gradescope.
A summary of the terminology we will use is on page 16 in the textbook.
Pre class reading for next time: Example 1.51, Definition 1.52
Notice: we are jumping to Section 1.3 Regular Expressions and then will come back to Section 1.1 Finite Automata on Friday.
Our motivation in studying sets of strings is that they encode problems.
We need to describe the collection of all strings that match the pattern or property of a problem.
Let’s start by thinking about how we can describe a language (a set of strings from a given alphabet).
Definition 1.52: A regular expression over alphabet \(\Sigma\) is a syntactic expression that can describe a language over \(\Sigma\). The collection of all regular expressions is defined recursively:
Basis steps of recursive definition
\(a\) is a regular expression, for \(a \in \Sigma\)
\(\varepsilon\) is a regular expression
\(\emptyset\) is a regular expression
Recursive steps of recursive definition
\((R_1 \cup R_2)\) is a regular expression when \(R_1\), \(R_2\) are regular expressions
\((R_1 \circ R_2)\) is a regular expression when \(R_1\), \(R_2\) are regular expressions
\((R_1^*)\) is a regular expression when \(R_1\) is a regular expression
The semantics (or meaning) of the syntactic regular expression is the language described by the regular expression. The function that assigns a language to a regular expression over \(\Sigma\) is defined recursively, using familiar set operations:
Basis steps of recursive definition
The language described by \(a\), for \(a \in \Sigma\), is \(\{a\}\) and we write \(L(a) = \{a\}\)
The language described by \(\varepsilon\) is \(\{\varepsilon\}\) and we write \(L(\varepsilon) = \{ \varepsilon\}\)
The language described by \(\emptyset\) is \(\{\}\) and we write \(L(\emptyset) = \emptyset\).
Recursive steps of recursive definition
When \(R_1\), \(R_2\) are regular expressions, the language described by the regular expression \((R_1 \cup R_2)\) is the union of the languages described by \(R_1\) and \(R_2\), and we write \[L(~(R_1 \cup R_2)~) = L(R_1) \cup L(R_2) = \{ w \mid w \in L(R_1) \lor w \in L(R_2)\}\]
When \(R_1\), \(R_2\) are regular expressions, the language described by the regular expression \((R_1 \circ R_2)\) is the concatenation of the languages described by \(R_1\) and \(R_2\), and we write \[L(~(R_1 \circ R_2)~) = L(R_1) \circ L(R_2) = \{ uv \mid u \in L(R_1) \land v \in L(R_2)\}\]
When \(R_1\) is a regular expression, the language described by the regular expression \((R_1^*)\) is the Kleene star of the language described by \(R_1\) and we write \[L(~(R_1^*)~) = (~L(R_1)~)^* = \{ w_1 \cdots w_k \mid k \geq 0 \textrm{ and each } w_i \in L(R_1)\}\]
For the following examples assume the alphabet is \(\Sigma_1 = \{0,1\}\):
The language described by the regular expression \(0\) is \(L(0) = \{ 0 \}\)
The language described by the regular expression \(1\) is \(L(1) = \{ 1 \}\)
The language described by the regular expression \(\varepsilon\) is \(L(\varepsilon) = \{ \varepsilon \}\)
The language described by the regular expression \(\emptyset\) is \(L(\emptyset) = \emptyset\)
The language described by the regular expression \(((0 \cup 1) \cup 1)\) is \(L(~((0 \cup 1) \cup 1)~) =\)
The language described by the regular expression \(1^+\) is \(L(~(1)^+~) =\)
The language described by the regular expression \(\Sigma_1^* 1\) is \(L(~\Sigma_1^* 1~) =\)
The language described by the regular expression \((\Sigma_1 \Sigma_1 \Sigma_1 \Sigma_1 \Sigma_1)^*\) is \(L(~(\Sigma_1 \Sigma_1 \Sigma_1 \Sigma_1 \Sigma_1)^*~) =\)
A regular expression that describes the language \(\{00, 01, 10, 11\}\) is
A regular expression that describes the language \(\{ 0^n1 \mid n~\text{is even} \}\) is
Shorthand and conventions
| Assuming \(\Sigma\) is the alphabet, we use the following conventions | |
|---|---|
| \(\Sigma\) | regular expression describing language consisting of all strings of length \(1\) over \(\Sigma\) |
| \(*\) then \(\circ\) then \(\cup\) | precedence order, unless parentheses are used to change it |
| \(R_1R_2\) | shorthand for \(R_1 \circ R_2\) (concatenation symbol is implicit) |
| \(R^+\) | shorthand for \(R^* \circ R\) |
| \(R^k\) | shorthand for \(R\) concatenated with itself \(k\) times, where \(k\) is a natural number |
| Pages 63 - 65 | |
Caution: many programming languages that support regular expressions build in functionality that is more powerful than the “pure” definition of regular expressions given here.
Regular expressions are everywhere (once you start looking for them).
Software tools and languages often have built-in support for regular expressions to describe patterns that we want to match (e.g. Excel/ Sheets, grep, Perl, python, Java, Ruby).
Under the hood, the first phase of compilers is to transform the strings we write in code to tokens (keywords, operators, identifiers, literals). Compilers use regular expressions to describe the sets of strings that can be used for each token type.
Next time: we’ll start to see how to build machines that decide whether strings match the pattern described by a regular expression.
Extra examples for practice:
Which regular expression(s) below describe a language that includes the string \(a\) as an element?
\(a^* b^*\)
\(a(ba)^* b\)
\(a^* \cup b^*\)
\((aaa)^*\)
\((\varepsilon \cup a) b\)
Please complete the review quiz questions on Gradescope about strings, languages, and regular expressions.
Recall: Review quizzes based on class material are assigned each day. These quizzes will help you track and confirm your understanding of the concepts and examples we work in class. Quizzes can be submitted on Gradescope as many times (with no penalty) as you like until the quiz deadline: the three quizzes each week are all due on Friday (with no penalty late submission open until Sunday).
The definition of the union, concatenation, and star operations for languages is given as Definition 1.23 on page 44 and a useful example is Example 1.24.
Pre class reading for next time: Figure 1.4, Definition 1.5
Notice: On Friday we are going back to the start of Chapter 1 and will be discussing finite automata and their computations.
Review: Determine whether each statement below about regular expressions over the alphabet \(\{a,b,c\}\) is true or false:
True or False: \(a \in L(~(a \cup b )~\cup c)\)
True or False: \(ab \in L(~ (a \cup b)^* ~)\)
True or False: \(ba \in L( ~ a^* b^* ~)\)
True or False: \(\varepsilon \in L(a \cup b \cup c)\)
True or False: \(\varepsilon \in L(~ (a \cup b)^* ~)\)
True or False: \(\varepsilon \in L( ~ a^* b^* ~)\)
From the pre-class reading, pages 34-36: A deterministic finite automaton (DFA) is specified by \(M = (Q, \Sigma, \delta, q_0, F)\). This \(5\)-tuple is called the formal definition of the DFA. The DFA can also be represented by its state diagram: with nodes for the state, labelled edges specifying the transition function, and decorations on nodes denoting the start and accept states.
Finite set of states \(Q\) can be labelled by any collection of distinct names. Often we use default state labels \(q0, q1, \ldots\)
The alphabet \(\Sigma\) determines the possible inputs to the automaton. Each input to the automaton is a string over \(\Sigma\), and the automaton “processes” the input one symbol (or character) at a time.
The transition function \(\delta\) gives the next state of the DFA based on the current state of the machine and on the next input symbol.
The start state \(q_0\) is an element of \(Q\). Each computation of the machine starts at the start state.
The accept (final) states \(F\) form a subset of the states of the DFA, \(F \subseteq Q\). These states are used to flag if the machine accepts or rejects an input string.
The computation of a machine on an input string is a sequence of states in the machine, starting with the start state, determined by transitions of the machine as it reads successive input symbols.
The DFA \(M\) accepts the given input string exactly when the computation of \(M\) on the input string ends in an accept state. \(M\) rejects the given input string exactly when the computation of \(M\) on the input string ends in a nonaccept state, that is, a state that is not in \(F\).
The language of \(M\), \(L(M)\), is defined as the set of all strings that are each accepted by the machine \(M\). Each string that is rejected by \(M\) is not in \(L(M)\). The language of \(M\) is also called the language recognized by \(M\).
What is finite about all deterministic finite automata? (Select all that apply)
The size of the machine (number of states, number of arrows)
The number of strings that are accepted by the machine
The length of each computation of the machine

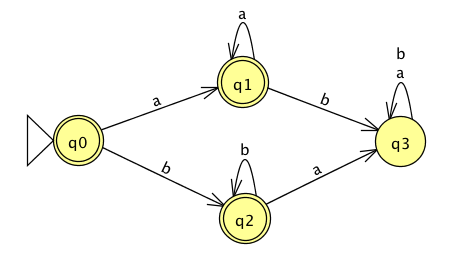
The formal definition of this DFA is
Classify each string \(a, aa, ab, ba, bb, \varepsilon\) as accepted by the DFA or rejected by the DFA.
Why are these the only two options?
The language recognized by this DFA is
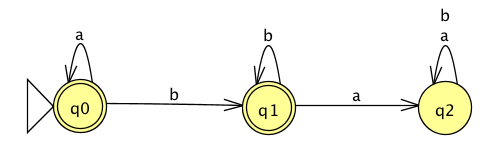
The language recognized by this DFA is
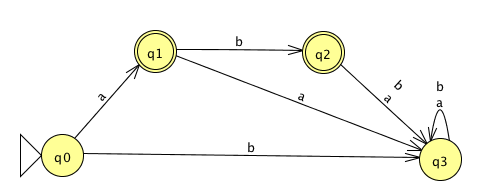
The language recognized by this DFA is
Please complete the review quiz questions on Gradescope about DFA and the strings they accept and reject.
The definition of the union, concatenation, and star operations for languages is given as Definition 1.23 on page 44 and a useful example is Example 1.24.
The first homework assignment for CSE 105 this quarter is due next week. Find it on the class website, direct link: https://theory-cs.github.io/website/assignments.html . Due: 4/7/22 at 5pm (no penalty late submission until 8am next morning)
We encourage you to work on homework in groups of up to three CSE 105 classmates. To find group members: reach out to people sitting around you in class, in discussion section, or during office hours. The pre-survey also asks if you want help finding group members: the CSE 105 instructional team can help you connect with other students. Working within the campus safety guidelines, you may choose to meet with your group mates in person or remotely. We highly recommend meeting synchronously so that you can work through the homework problems *together*.
Pre class reading for next time: pages 41-43 (figures 1.18, 1.19, 1.20)
Page references are to the 3rd edition (International) of Siper’s Introduction to the Theory of Computation, available at the campus bookstore for under $20. Copies of the book are also available for those who can’t access the book to borrow from the course instructor, while supplies last (minnes@eng.ucsd.edu)↩︎