(Graded for correctness1)
Give an example of a decidable language \(L_1\) whose complement is also decidable. A complete solution will include either (1) a precise definition of the example language \(L_1\) and an explanation of why it is decidable and why its complement is decidable, or (2) a sufficiently general and correct argument for why there is no way to choose an example language to satisfy this requirement. All justifications and arguments should connect to the relevant definitions and the specific concepts being discussed.
Give an example of a decidable language \(L_2\) and a Turing machine \(M_2\) such that \(L(M_2) = L_2\) but \(M_2\) does not decide \(L_2\). A complete solution will include either (1) precise definitions of \(L_2\) and \(M_2\) and justifications for why \(L(M_2) = L_2\) and why \(M_2\) does not decide \(L_2\), or (2) a sufficiently general and correct argument for why there is no way to choose such a language and machine. For any machines you discuss, you can choose whether to use high-level descriptions, implementation level descriptions, or formal definitions. All justifications and arguments should connect to the relevant definitions and the specific concepts being discussed.
(Graded for fair effort completeness2)
Recall that a set \(X\) is said to be closed under an operation \(OP\) if, for any elements in \(X\), applying \(OP\) to them gives an element in \(X\). For example, the set of integers is closed under multiplication because if we take any two integers, their product is also an integer.
Suppose \(M_1\) and \(M_2\) are Turing machines. Consider the following high-level descriptions of machines that give general constructions based on \(M_1\) and \(M_2\).
Consider the following construction of a nondeterministic Turing machine:
“On input \(w\)
Nondeterministically split \(w\) into two pieces, i.e. choose \(x,y\) such that \(w = xy\).
Simulate running \(M_1\) on \(x\).
Simulate running \(M_2\) on \(y\).
If both simulations in steps 2 and 3 accept, accept."
Can this construction be used to prove that the class of Turing-recognizable languages is closed under concatenation? Briefly justify your answer.
Consider the following construction of an enumerator:
“Without any input
Build an enumerator \(E_1\) that is equivalent to \(M_1\).
Build an enumerator \(E_2\) that is equivalent to \(M_2\).
Start \(E_1\) running and start \(E_2\) running.
Initialize a list of all strings that have been printed by \(E_1\). Declare the variable \(n_1\) to be the length of this list (initially \(n_1 = 0\)).
Initialize a list of all strings that have been printed by \(E_2\) so far. Declare the variable \(n_2\) to be the length of this list (initially \(n_2 = 0\)).
Every time a new string \(x\) is printed by \(E_1\):
Add this string to the list of strings printed by \(E_1\) so far.
Increment \(n_1\) so it stores the current length of the list.
For \(j = 1 \ldots n_2\),
Let \(w_j\) be the \(j\)th string in the list of strings printed by \(E_2\)
Print \(xw_j\).
Every time a new string \(y\) is printed by \(E_2\):
Add this string to the list of strings printed by \(E_2\) so far.
Increment \(n_2\) so it stores the current length of the list.
For \(i = 1 \ldots n_1\),
Let \(u_i\) be the \(i\)th string in the list of strings printed by \(E_1\)
Print \(u_i y\)."
Can this construction be used to prove that the class of Turing-recognizable languages is closed under concatenation? Briefly justify your answer.
Consider the following construction of a Turing machine:
“On input \(w\)
Let \(n = |w|\).
Create a two dimensional array of strings \(s_{m,j}\) where \(0 \leq m \leq n\) and \(0 \leq j \leq 1\).
For each \(0 \leq m \leq n\), initialize \(s_{m,0}\) to be the prefix of \(w\) of length \(m\) and \(s_{m,1}\) to be the suffix of \(w\) of length \(n-m\). In other words, \(w= s_{m,0} s_{m,1}\) and \(|s_{m,0}| = m\), \(|s_{m,1}| = n-m\).
For \(i = 1, 2, \ldots\)
For \(k = 0, \ldots, i\)
Run \(M_1\) on \(s_{\min{(k,n)},0}\) for (at most) \(i\) steps.
Run \(M_2\) on \(s_{\min{(k,n)},1}\) for (at most) \(i\) steps.
If both simulations in steps 6 and 7 accept, accept."
Can this construction be used to prove that the class of Turing-recognizable languages is closed under concatenation? Briefly justify your answer.
(Graded for fair effort completeness) Recall that \[A_{TM} = \{ \langle M, w \rangle \mid \text{$M$ is a Turing machine, $w$ is a string, and $w \in L(M)$} \}\] and \[HALT_{TM} = \{ \langle M, w \rangle \mid \text{$M$ is a Turing machine, $w$ is a string, and $M$ halts on $w$}\}\]
Consider the Turing machines below, with input alphabet \(\Sigma = \{0,1\}\), tape alphabet \(\{0, 1, \textvisiblespace\}\), and state diagrams (with the usual conventions):
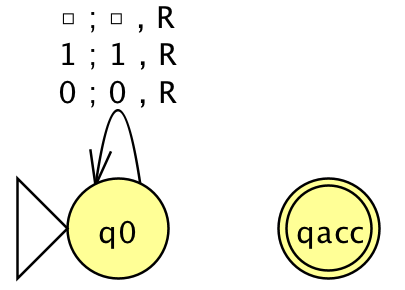
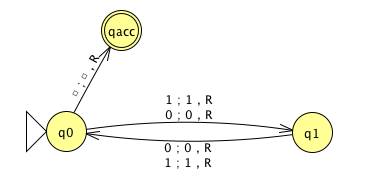
Give an example string that is in both \(A_{TM}\) and \(HALT_{TM}\) and that is related to one of the two Turing machines whose state diagrams are given above, or explain why there is no such string.
Give an example string that is in \(A_{TM}\) and is not in \(HALT_{TM}\) and that is related to one of the two Turing machines whose state diagrams are given above, or explain why there is no such string.
Give an example string that is not in \(A_{TM}\) and is in \(HALT_{TM}\) and that is related to one of the two Turing machines whose state diagrams are given above, or explain why there is no such string.
(Graded for correctness) Fix \(\Sigma = \{0,1\}\) for this question. For each part below, you can choose sets from the following list: \[\emptyset, A_{TM}, \overline{A_{TM}}, HALT_{TM}, \overline{HALT_{TM}}, E_{TM}, \overline{E_{TM}}, EQ_{TM}, \overline{EQ_{TM}}, \Sigma^*\] You may use each set from the list at most once in the examples below. In particular, you can’t choose \(A = B = C = D = X = Y = \Sigma^*\).
Find sets \(A, B\) for which the computable function \[\begin{aligned} F &= \text{``On input $x$} \\ &\text{1. Output $\langle \includegraphics[width=0.5in]{../../resources/machines/Lect22TM1.png} , 00\rangle$."} \end{aligned}\]
witnesses the mapping reduction \(A \leq_m B\). Justify your answer by proving that, for all strings \(x\), \(x \in A\) iff \(F(x) \in B\). If no such sets exist, justify why not.
Find sets \(C, D\) for which the computable function \[\begin{aligned} G &= \text{``On input $x$} \\ &\text{1. Check if $x = \langle M, w \rangle$ for $M$ a Turing machine and $w$ a string. If so, go to step 3.}\\ &\text{2. If not, output $\langle \includegraphics[width=0.5in]{../../resources/machines/hw5tm1.png}, \includegraphics[width=1in]{../../resources/machines/Lect22TM2.png} \rangle$.}\\ &\text{3. Construct the Turing machine $M'_x = $ ``On input $y$,} \\ &\text{\qquad 1. If $y$ has a positive and odd length, reject.}\\ &\text{\qquad 2. Else, if $y$ has a positive and even length, accept.}\\ &\text{\qquad 3. Otherwise, run $M$ on $w$ and, if the computation halts, accept $y$."}\\ &\text{4. Output $\langle M'_x , \includegraphics[width=1in]{../../resources/machines/Lect22TM2.png}\rangle$."} \end{aligned}\]
witnesses the mapping reduction \(C \leq_m D\). Justify your answer by proving that, for all strings \(x\), \(x \in C\) iff \(G(x) \in D\). If no such sets exist, justify why not.
Find sets \(X, Y\) for which the computable function \[\begin{aligned} H &= \text{``On input $x$} \\ &\text{1. Check if $x = \langle M, w \rangle$ for $M$ a Turing machine and $w$ a string. If so, go to step 3.}\\ &\text{2. If not, output $\langle \includegraphics[width=1in]{../../resources/machines/hw5tm2.png}\rangle$.}\\ &\text{3. Construct the Turing machine $M'_x = $ ``On input $y$,} \\ &\text{\qquad 1. If $y \neq w$, reject.}\\ &\text{\qquad 2. Otherwise, run $M$ on $w$.}\\ &\text{\qquad 3. If $M$ accepts, accept. If $M$ rejects, reject."} \\ &\text{4. Output $\langle M'_x \rangle$."} \end{aligned}\]
witnesses a mapping reduction \(X \leq_m Y\). Justify your answer by proving that, for all strings \(x\), \(x \in X\) iff \(H(x) \in Y\). If no such sets exist, justify why not.