For this question, we are working over the fixed alphabet \(\{a,b,c\}\).
(Graded for fair effort completeness1)
Consider the PDA over this alphabet with state diagram
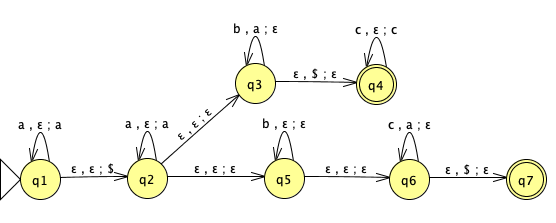
Give an informal description of this PDA and describe the language it recognizes using set builder notation.
Hint: Compare the PDA with the machine in Example 2.16 and Figure 2.17 of the textbook (page 116), which recognizes the language \(\{a^i b^j c^k \mid i,j,k \geq 0 \textrm{ and } i=j \textrm{ or } i=k\}\) and identify the main differences.
(Graded for correctness2)
Consider the CFG \((\{X, S, S_1, S_2, T, Y\}, \{a,b,c\}, R, X)\) where the set of rules \(R\) has \[\begin{aligned} X &\to aX \mid S \mid T \\ S &\to S_1S_2 \\ S_1 &\to aS_1 b \mid \varepsilon \\ S_2 &\to cS_2 \mid \varepsilon\\ T &\to aTc \mid Y \\ Y &\to bY \mid \varepsilon \end{aligned}\]
For each of the following strings, either give a derivation in this grammar that proves the string is in the language generated by the grammar, or explain why there is no such derivation.
\(aaaa\)
\(abbc\)
\(aabb\)
(Graded for correctness) Modify the start variable of this context-free grammar to get a different CFG (with the same set of variables, set of terminals, and set of rules) that generates an infinite regular language, if possible. A complete solution will include either (1) the formal definition of this new CFG and an explanation of why the language it recognizes is both infinite and regular, or (2) a sufficiently general and correct argument for why there is no way to choose the start variable to satisfy this requirement.
(Graded for correctness) In this question, you’ll practice working with formal general constructions for PDAs and translating between state diagrams and formal definitions.
Suppose \[M = (Q, \Sigma, \Gamma, \delta, q_0, F)\] is a PDA. We can define a new PDA \(N\) so that \(L(M) = L(N)\) and \(N\) is guaranteed to have an empty stack at the end of any accepting computation. Informally, the construction is as follows: Add three new states \(q_1', q_2', q_3'\) and one new stack symbol \(\#\).
One of the new states \(q_1'\) will be the new start state and it has a spontaneous transition to the old start state \(q_0\) which pushes the new stack symbol \(\#\) to the stack.
The transitions between the old states are all the same.
From each of the old accept states, add a spontaneous transition (that doesn’t modify the stack) to the second new state \(q_2'\).
In this state \(q_2'\), pop all old stack symbols from the stack without reading any input.
When the new stack symbol \(\#\) is on the top of the stack, transition to the third new state \(q_3'\) and accept.
Assume \(\{ q_1', q_2', q_3'\} \cap Q = \emptyset\) (otherwise, relabel some of the states in \(Q\)) and assume that \(\# \notin \Gamma\) (otherwise, relabel this stack symbol in \(\Gamma\)). Define \(N\) to be \[N = ( Q \cup \{ q_1', q_2', q_3'\} , \Sigma, \Gamma \cup \{\#\}, \delta_N, q_1', \{q_3'\} )\] where \(\delta_N : Q \cup \{ q_1', q_2', q_3'\}~~\times~~ \Sigma_\varepsilon ~~\times~~\Gamma_\varepsilon\cup \{\#\} \to \mathcal{P}( Q \cup \{ q_1', q_2', q_3'\} ~~\times ~~\Gamma_\varepsilon\cup \{\#\})\) is defined as \[\delta_N ( ~(q, x, y)~) = \begin{cases} \{ (q_0, \#) \} &\qquad \text{if $q = q_1'$, $x = \varepsilon$, $y = \varepsilon$} \\ \delta( ~(q, x, y)~) & \qquad \text{if $q \in Q$, $x \in \Sigma$, $y \in \Gamma_\varepsilon$} \\ \delta( ~(q, x, y)~) & \qquad \text{if $q \in Q$, $x=\varepsilon$, $y \in \Gamma$} \\ \delta( ~(q, x, y)~) & \qquad \text{if $q \in Q \setminus F$, $x=\varepsilon$, $y =\varepsilon$} \\ \delta( ~(q, x, y)~) \cup \{ (q_2', \varepsilon) \} & \qquad \text{if $q \in F$, $x=\varepsilon$, $y =\varepsilon$} \\ \{ (q_2', \varepsilon)\} & \qquad \text{if $q = q_2'$, $x = \varepsilon$, $y \in \Gamma$} \\ \{ (q_3', \varepsilon)\} & \qquad \text{if $q = q_2'$, $x = \varepsilon$, $y = \#$} \\ \emptyset & \qquad \text{otherwise} \end{cases}\]
(Graded for correctness) Illustrate this construction by considering the PDA \(M\) over the input alphabet \(\{a,b,c\}\)

and applying the construction above to create the related PDA \(N\) and include its state diagram in your submission. Note: you may include the formal definition of your PDA, but this is not required.
(Graded for correctness) Pick a string of length \(5\) over the alphabet of the PDA \(M\) and use it to demonstrate the difference in \(M\) and in \(N\) by
describing an accepting computation of \(M\) on this string for which the stack is not empty at the end of the computation, and
describing an accepting computation of \(N\) on this string for which the stack is empty at the end of the computation.
In your descriptions of these computations, include both the sequence of states visited by the machine as well as snapshots of the full contents of the stack at each step in the computation. You may hand-draw and scan these traces of the computations.
Hint: You will need to pick your example string wisely. It must be accepted by \(M\) and there must be a computation of \(M\) on your string which ends with a nonempty stack. Not all choices of length \(5\) strings work.
(Graded for fair effort completeness)
Fix an arbitrary alphabet \(\Sigma\). Prove that the class of context-free languages over \(\Sigma\) is closed under concatenation in two ways:
Prove that, for any languages \(L_1, L_2\) over \(\Sigma\), if there are PDAs \(M_1\) and \(M_2\) such that \(L_1 = L(M_1)\) and \(L_2 = L(M_2)\), then there is a PDA that recognizes \(L_1 \circ L_2\).
Prove that, for any languages \(L_1, L_2\) over \(\Sigma\), if there are CFGs \(G_1\) and \(G_2\) such that \(L_1 = L(G_1)\) and \(L_2 = L(G_2)\), then there is a CFG that generates \(L_1 \circ L_2\).
Consider the Turing machine \(T\) over the input alphabet \(\Sigma = \{0,1\}\) with the state diagram below (the tape alphabet is \(\Gamma = \{ 0,1,X,\square\}\)). Convention: any missing transitions in the state diagram have value \((qrej,\square,R)\)
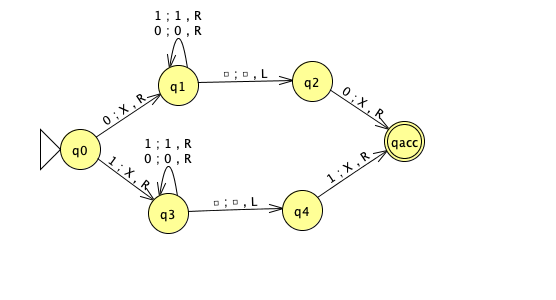
(Graded for correctness) Specify an example string \(w_1\) of length \(4\) over \(\Sigma\) that is accepted by this Turing machine, or explain why there is no such example. A complete solution will include either (1) a precise and clear description of your example string and a precise and clear description of the accepting computation of the Turing machine on this string or (2) a sufficiently general and correct argument why there is no such example, referring back to the relevant definitions.
To describe a computation of a Turing machine, include the contents of the tape, the state of the machine, and the location of the read/write head at each step in the computation.
Hint: In class we’ve drawn pictures to represent the configuration of the machine at each step in a computation. You may do so or you may choose to describe these configurations in words.
(Graded for correctness) Specify an example string \(w_2\) of length \(3\) over \(\Sigma\) that is rejected by this Turing machine or explain why there is no such example. A complete solution will include either (1) a precise and clear description of your example string and a precise and clear description of the rejecting computation of the Turing machine on this string or (2) a sufficiently general and correct argument why there is no such example, referring back to the relevant definitions.
(Graded for correctness) Specify an example string \(w_3\) of length \(2\) over \(\Sigma\) on which the computation of this Turing machine loops or explain why there is no such example. A complete solution will include either (1) a precise and clear description of your example string and a precise and clear description of the looping (non-halting) computation of the Turing machine on this string or (2) a sufficiently general and correct argument why there is no such example, referring back to the relevant definitions.
(Graded for fair effort completeness) Write an implementation level description of the Turing machine \(T\).