(Graded for fair effort completeness1) Do the following for each of the following attempted “proofs" that a set is nonregular:
Find the (first and/or most significant) logical error in the “proof" and describe why it’s wrong.
Either prove that the set is actually regular (by finding a regular expression that describes it or a DFA/NFA that recognizes it, and justifying why) or fix the proof so that it is logically sound.
The language \(X_1 = \{ uw \mid \text{$u$ and $w$ are strings over $\{0,1\}$ and have the same length} \}\).
“Proof" that \(X_1\) is not regular using the Pumping Lemma: Let \(p\) be an arbitrary positive integer. We will show that \(p\) is not a pumping length for \(X_1\).
Choose \(s\) to be the string \(1^p 0^p\), which is in \(X_1\) because we can choose \(u = 1^p\) and \(w = 0^p\) which each have length \(p\). Since \(s\) is in \(X_1\) and has length greater than or equal to \(p\), if \(p\) were to be a pumping length for \(X_1\), \(s\) ought to be pump’able. That is, there should be a way of dividing \(s\) into parts \(x,y,z\) where \(s=xyz\), \(|y| >0\), \(|xy| \leq p\), and for each \(i \geq 0\), \(xy^iz \in X_1\). Suppose \(x,y,z\) are such that \(s = xyz\), \(|y| > 0\) and \(|xy| \leq p\). Since the first \(p\) letters of \(s\) are all \(1\) and \(|xy| \leq p\), we know that \(x\) and \(y\) are made up of all \(1\)s. If we let \(i=2\), we get a string \(xy^iz\) that is not in \(X_1\) because repeating \(y\) twice adds \(1\)s to \(u\) but not to \(w\), and strings in \(X_1\) are required to have \(u\) and \(w\) be the same length. Thus, \(s\) is not pumpable (even though it should have been if \(p\) were to be a pumping length) and so \(p\) is not a pumping length for \(X_1\). Since \(p\) was arbitrary, we have demonstrated that \(X_1\) has no pumping length. By the Pumping Lemma, this implies that \(X_1\) is nonregular.
The language \(X_2 = \{ u0w \mid \text{$u$ and $w$ are strings over $\{0,1\}$ and have the same length} \}\).
“Proof" that \(X_2\) is not regular using the Pumping Lemma: Let \(p\) be an arbitrary positive integer. We will show that \(p\) is not a pumping length for \(X_2\).
Choose \(s\) to be the string \(1^{p} 0^{p+1}\), which is in \(X_2\) because we can choose \(u = 1^p\) and \(w = 0^p\) which each have length \(p\). Since \(s\) is in \(X_2\) and has length greater than or equal to \(p\), if \(p\) were to be a pumping length for \(X_2\), \(s\) ought to be pump’able. That is, there should be a way of dividing \(s\) into parts \(x,y,z\) where \(s=xyz\), \(|y| >0\), \(|xy| \leq p\), and for each \(i \geq 0\), \(xy^iz \in X_2\). When \(x = \varepsilon\) and \(y = 1^{p}\) and \(z = 0^{p+1}\), we have satisfied that \(s = xyz\), \(|y| > 0\) (because \(p\) is positive) and \(|xy| \leq p\). If we let \(i=2\), we get the string \(xy^iz = 1^{2p}0^{p+1}\) that is not in \(X_2\) because its middle symbol is a \(1\), not a \(0\). Thus, \(s\) is not pumpable (even though it should have been if \(p\) were to be a pumping length) and so \(p\) is not a pumping length for \(X_2\). Since \(p\) was arbitrary, we have demonstrated that \(X_2\) has no pumping length. By the Pumping Lemma, this implies that \(X_2\) is nonregular.
(Graded for correctness2) Give an example of a language over the alphabet \(\{a,b,c\}\) that has cardinality \(2\) and for which \(4\) is a pumping length and \(3\) is not a pumping length. A complete solution will give a clear and precise description of the language, a justification for why \(4\) is a pumping length, and a justification for why \(3\) is not a pumping length.
(Graded for fair effort completeness) Prove or disprove each of the following statements. (In other words, decide whether each statement is true or false and justify your decision.) Fix \(\Sigma\) an arbitrary (but unknown) alphabet.
If a language \(L\) over \(\Sigma\) is nonregular then its complement \(\overline{L}\) is regular.
Each nonregular language over \(\Sigma\) is infinite.
For each \(w \in \Sigma^*\), there is a regular language \(L_{w}\) such that \(w \in L_{w}\).
For each \(w \in \Sigma^*\), there is a nonregular language \(L_{w}\) such that \(w \in L_{w}\).
If a language over \(\Sigma\) is recognized by a PDA then it is nonregular.
(Graded for correctness) In the first week’s homework, we saw the definitions of two functions on the set of languages over \(\{0,1\}\): for \(L\) a set of strings over the alphabet \(\{0,1\}\), we can define the following associated sets \[LZ(L) = \{ 0^k w \mid w \in L, k \in \mathbb{Z}, k \geq 0 \}\] \[TZ(L) = \{ w 0^k \mid w \in L, k \in \mathbb{Z}, k \geq 0 \}\] This week we’ll just focus on \(LZ(L)\). In class and in the reading so far, we’ve seen the following examples of nonregular languages:
3
\(\{ 0^n 1^n ~|~ n \geq 0 \}\) \[\{ 0^n 1^n ~|~ n \geq 2 \}\] \[\{ 0^n 1^m ~|~ 0 \leq n \leq m \}\] \[\{ 0^n 1^m ~|~ 0 \leq m \leq n \}\] \[\{ 0^n 1^{2n} ~|~ 0 \leq n \}\] \[\{ 0^n 1^{n+1} ~|~ 0 \leq n \}\] \[\{ 1^{n^2} ~|~ 0 \leq n \}\] \[\{ 0^n 1^m 0^n ~|~n,m \geq 0\}\] \[\{ w \in \{0,1\}^* ~|~w = w^R\}\] \[\{ w w^R ~|~ w \in \{0,1\}^*\}\]
Use (some of) the sets above, along with any regular sets you would like, to prove or disprove the statement: “The class of nonregular languages is closed under the function \(LZ\).”
A complete solution will include a precise description of whether the statement is true or false, referring back to the definition of closure, the definition of the function \(LZ\), and the definition of nonregularity. You may use any claims we proved in class or that are proved in the textbook reading, so long as you reference them clearly in your argument by referring to a specific page in the notes, timestamp of a video, or page in the book.
Bonus; not for credit: extend this homework problem for \(TZ(L)\) as well.
Consider the PDA with input alphabet \(\Sigma = \{ 0, 1\}\) and stack alphabet \(\Gamma = \{\$, X\}\) and the following state diagram
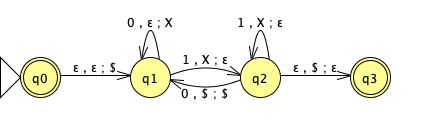
(Graded for correctness) Specify an example string \(w_1\) over \(\Sigma\) that is accepted by this PDA, or explain why there is no such example. A complete solution will include either (1) a precise and clear description of your example string and a precise and clear description of the accepting computation of the PDA on this string (potentially using diagrams like those we used in class when tracing PDA computations) or (2) a sufficiently general and correct argument why there is no such example, referring back to the relevant definitions.
(Graded for correctness) Specify an example string \(w_2\) over \(\Sigma\) that is not accepted by this PDA, or explain why there is no such example. A complete solution will include either (1) a precise and clear description of your example string and a precise and clear description of all possible computations of the PDA on this string (potentially using diagrams like those we used in class when tracing PDA computations) to show that none of them are accepting or (2) a sufficiently general and correct argument why there is no such example, referring back to the relevant definitions.
(Graded for completeness) Is the language recognized by this PDA regular or nonregular? You might find it useful to first write out this language in set notation.
(Graded for completeness) Modify the set of accept states of this state diagram to get a different PDA (with the same set of states, input alphabet, stack alphabet, start state, and transition function) that recognizes an infinite regular language, if possible. A complete solution will include either (1) the diagram of this new PDA and an explanation of why the language it recognizes is both infinite and regular, or (2) a sufficiently general and correct argument for why there is no way to choose the set of accept states to satisfy this requirement.