(Graded for correctness1) Over the alphabet \(\{a,b\}\), consider the language \[L = \{ w \in \{a,b\}^* \mid (ab \textrm{ is a substring of $w$}) \land (ba \textrm{ is a substring of $w$}) \land (w \textrm{ starts with } a)\}\] In this question, you will use two different approaches to proving that this language is regular by building (different) DFA that recognize this language.
Design a DFA recognizing the language \(\{ w \in \{a,b\}^* \mid ab \textrm{ is a substring of $w$}\}\) and a DFA recognizing the language \(\{ w \in \{a,b\}^* \mid ba \textrm{ is a substring of $w$}\}\) and a third DFA recognizing the language \(\{ w \in \{a,b\}^* \mid w \textrm{ starts with } a\}\). Then, use the construction we discussed in class to combine these DFA to get a DFA that recognizes \(L\). A complete solution will include the (clearly labelled) state diagrams for each of the three building-block DFAs, along with a description of the result of combining these DFAs that includes the formal definition of the resulting DFA and at the least the part of the state diagram that includes the start state, all the outgoing edges from the start state, and specifies how many states the full DFA will have.
Rewrite the language \(L\) in a simpler form and use this simpler form to design a DFA with at most \(5\) states that recognizes \(L\). A complete solution will include the complete state diagram of this DFA and a justification for why the DFA recognizes \(L\).
To safeguard the privacy or security of a network, some software filters the IP addresses that are allowed to send content to computers on the network. Each IP address can be broken into parts that represent the source host of incoming traffic, including geographic data. As a result, software needs to be designed to recognize whether certain substrings (representing permitted hosts) are present (if the hosts are permitted to send data) and whether others are absent (if those hosts are blocked from sending data).
In this question, you’ll design ways to detect these patterns in strings.
(Graded for correctness) Over the alphabet \(\{0,1,2,3,4,5,6,7,8,9\}\) design a DFA that accepts each and only strings that have \(384\) or \(116\) as a substring. Your DFA should have no more than \(8\) states. A complete solution will include the state diagram of your DFA and a brief justification of your construction by explaining the role each state plays in the machine. Note: you may include the formal definition of your DFA, but this is not required.
(Graded for correctness) Now suppose the network administrators want to block traffic from IP addresses that have been associated with spammers. Over the alphabet \(\{0,1,2,3,4,5,6,7,8,9\}\), design an NFA with at most \(5\) states that accepts each and only strings that do not have the substring \(384\) and do not have the substring \(116\). A complete solution will include the state diagram of your NFA and a brief justification of your construction by explaining the role each state plays in the machine.
(Graded for fair effort completeness2) Give a regular expression that describes the set of strings over the alphabet \(\{0,1,2,3,4,5,6,7,8,9\}\) that have \(384\) as a substring and give a (different) regular expression that describes the set of strings over the alphabet \(\{0,1,2,3,4,5,6,7,8,9\}\) that do not have \(384\) as a substring. Briefly justify why each of your regular expression works.
In this question, you’ll practice working with formal general constructions for DFAs and translating between state diagrams and formal definitions. Consider the following construction in the textbook for Chapter 1 Problem 34, which we include here for reference: “Let \(B\) and \(C\) be languages over \(\Sigma = \{ 0,1\}\). Define \[B \overset{1}{\leftarrow} C= \{ w \in B ~\mid~\textrm{ for some $y \in C$, strings $w$ and $y$ contain equal numbers of $1$s }\}\] The class of regular languages is shown to be closed under the \(\overset{1}{\leftarrow}\) operation using the construction: Let \(M_B = (Q_B, \Sigma, \delta_B, q_B, F_B)\) and \(M_C = ( Q_C, \Sigma, \delta_C, q_C, F_C)\) be DFAs recognizing the languages \(B\) and \(C\), respectively. We will now construct NFA \(M = (Q, \Sigma, \delta, q_0, F)\) that recognizes \(B \overset{1}{\leftarrow} C\) as follows. To decide whether its input \(w\) is in \(B \overset{1}{\leftarrow} C\), the machine \(M\) checks that \(w \in B\), and in parallel nondeterministically guesses a string \(y\) that contains the same number of \(1\)s as contained in \(w\) and checks that \(y \in C\).
\(Q = Q_B \times Q_C\)
For \((q,r) \in Q\) and \(a \in \Sigma_\varepsilon\), define \[\delta( ~((q,r), a)~) = \begin{cases} \{ (\delta_B(q,0) , r ) \} \qquad&\textrm{if } a = 0 \\ \{ (\delta_B( q,1) , \delta_C( r,1) ) \} \qquad&\textrm{if } a = 1 \\ \{ (q, \delta_C( r,0 ))\} \qquad&\textrm{if } a = \varepsilon\\ \end{cases}\]
\(q_0 = (q_B, q_C)\)
\(F = F_B \times F_C\) ."
(Graded for correctness) Illustrate this construction by defining specific example DFAs \(M_B\) and \(M_C\) and including their state diagrams in your submission. Choose \(M_B\) to have four states and \(M_C\) to have two states, and make sure that every state in each state diagram is reachable from the start state of that machine. Apply the construction above to create the NFA \(M\) and include its state diagram in your submission. Note: you may include the formal definition of your DFAs and NFA, but this is not required.
Hint: Confirm that you have specified every required piece of the state diagram for \(M\). E.g., label the states consistently with the construction, indicate the start arrow, specify each accepting state, and include all required transitions.
(Graded for fair effort completeness) Describe the sets recognized by each of the machines you used in part (a): \(M_B, M_C, M\). If possible, give an example of a string that is in \(B\) and in \(B \overset{1}{\leftarrow} C\) and an example of a string that is in \(B\) and not in \(B \overset{1}{\leftarrow} C\). If any of these examples do not exist, explain why not.
(Graded for fair effort completeness) In last week’s homework, we saw the definitions of two functions on the set of languages over \(\{0,1\}\): for \(L\) a set of strings over the alphabet \(\{0,1\}\), we can define the following associated sets \[LZ(L) = \{ 0^k w \mid w \in L, k \in \mathbb{Z}, k \geq 0 \}\] \[TZ(L) = \{ w 0^k \mid w \in L, k \in \mathbb{Z}, k \geq 0 \}\] In this question, we’ll develop a general construction that will prove that if \(L\) is regular then so are \(LZ(L)\) and \(TZ(L)\).
Consider an arbitrary regular language \(L\) over the alphabet \(\Sigma = \{0,1\}\), and we are given that \(M = (Q, \Sigma, \delta, q_0, F)\) is a DFA over \(\Sigma\) with \(L(M) = L\).
Give the formal construction of an NFA \(M'\) with \(L(M') = LZ(L)\). Briefly justify each parameter in the definition of \(M'\).
Apply your construction from part (a) when \(L_{test} = L(M_{test})\), where the state diagram \(M_{test}\) is below. Submit the state diagram of the NFA that results. If possible, give an example of a string that is in \(LZ(L_{test})\) and one that is not; if either of these examples do not exist, explain why not.
Give the formal construction of an NFA \(N'\) with \(L(N') = TZ(L)\). Briefly justify each parameter in the definition of \(N'\).
Apply your construction from part (c) when \(L_{test} = L(M_{test})\), where the state diagram \(M_{test}\) is below. Submit the state diagram of the NFA that results. If possible, give an example of a string that is in \(TZ(L_{test})\) and one that is not; if either of these examples do not exist, explain why not.
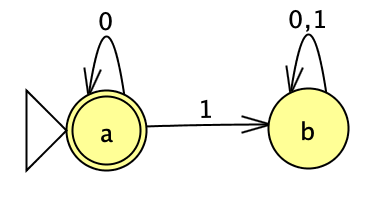
State diagram for DFA \(M_{test}\)
Caution: Pay attention to the types of the components, especially in the transition function. You are given a DFA and are building an NFA.