HW1 : Regular Expressions and Deterministic Finite Automata

In this assignment,

You will practice reading and applying the definitions of alphabets, strings, languages, Kleene star, and regular expressions. You will use regular expressions and relate them to languages and automata. You will use precise notation to formally define the state diagram of DFA, and you will use clear English to describe computations of DFA informally.

Resources: To review the topics you are working with for this assignment, see the class material from Week 1. We will post frequently asked questions and our answers to them in a pinned Piazza post.

Reading and extra practice problems: Sipser Section 0, 1.3, 1.1. Chapter 1 exercises 1.1, 1.2, 1.3, 1.18, 1.23.

For all HW assignments:

Weekly homework may be done individually or in groups of up to 3 students. You may switch HW partners for different HW assignments. The lowest HW score will not be included in your overall HW average. Please ensure your name(s) and PID(s) are clearly visible on the first page of your homework submission and then upload the PDF to Gradescope. If working in a group, submit only one submission per group: one partner uploads the submission through their Gradescope account and then adds the other group member(s) to the Gradescope submission by selecting their name(s) in the “Add Group Members" dialog box. You will need to re-add your group member(s) every time you resubmit a new version of your assignment. Each homework question will be graded either for correctness (including clear and precise explanations and justifications of all answers) or fair effort completeness. You may only collaborate on HW with CSE 105 students in your group; if your group has questions about a HW problem, you may ask in drop-in help hours or post a private post (visible only to the Instructors) on Piazza.

All submitted homework for this class must be typed. You can use a word processing editor if you like (Microsoft Word, Open Office, Notepad, Vim, Google Docs, etc.) but you might find it useful to take this opportunity to learn LaTeX. LaTeX is a markup language used widely in computer science and mathematics. The homework assignments are typed using LaTeX and you can use the source files as templates for typesetting your solutions. To generate state diagrams of machines, we recommend using Flap.js or JFLAP. Photographs of clearly hand-drawn diagrams may also be used. We recommend that you submit early drafts to Gradescope so that in case of any technical difficulties, at least some of your work is present. You may update your submission as many times as you’d like up to the deadline.

Integrity reminders

• Problems should be solved together, not divided up between the partners. The homework is designed to give you practice with the main concepts and techniques of the course, while getting to know and learn from your classmates.

• You may not collaborate on homework with anyone other than your group members. You may ask questions about the homework in office hours (of the instructor, TAs, and/or tutors) and on Piazza (as private notes viewable only to the Instructors). You cannot use any online resources about the course content other than the class material from this quarter – this is primarily to ensure that we all use consistent notation and definitions we will use this quarter and also to protect the learning experience you will have when the ‘aha’ moments of solving the problem authentically happen.

• Do not share written solutions or partial solutions for homework with other students in the class who are not in your group. Doing so would dilute their learning experience and detract from their success in the class.

You will submit this assignment via Gradescope (https://www.gradescope.com) in the assignment called “HW1CSE105Sp22”.

Assigned questions

1. (Graded for correctness¹) For \(L\) a set of strings over the alphabet \(\{0,1\}\), we can define the following associated sets \[LZ(L) = \{ 0^k w \mid w \in L, k \in \mathbb{Z}, k \geq 0 \}\] \[TZ(L) = \{ w 0^k \mid w \in L, k \in \mathbb{Z}, k \geq 0 \}\]

   Note: the commas in the set-builder definition indicate “and”.

   Note: \(0^k\) is the result of concatenating \(0\) with itself \(k\) times; it is the string of \(k\) \(0\)s.

   Note: Formally, \(LZ\) and \(TZ\) are each functions, with domain the set of languages over \(\{0,1\}\) and with codomain the set of languages over \(\{0,1\}\).

   1. Specify an example language \(L_1\) over \(\{0,1\}\) where \(LZ(L_1) = \Sigma^*\), or explain why there is no such example. A complete solution will include either (1) a precise and clear description of your example language \(L_1\) and a precise and clear description of the result of computing \(LZ(L_1)\) using the definitions to justify this description and justifying the set equality with \(\Sigma^*\), or (2) a sufficiently general and correct argument why there is no such example, referring back to the relevant definitions.

   2. Specify an example language \(L_2\) over \(\{0,1\}\) where \(LZ(L_2)\) is a finite set, or explain why there is no such example. A complete solution will include either (1) a precise and clear description of your example language \(L_2\) and a precise and clear description of the result of computing \(LZ(L_2)\) using the definitions to justify this description and justifying why it is finite, or (2) a sufficiently general and correct argument why there is no such example, referring back to the relevant definitions.

   3. Specify an example language \(L_3\) over \(\{0,1\}\) where \(LZ(L_3) = TZ(L_3)\), or explain why there is no such example. A complete solution will include either (1) a precise and clear description of your example language \(L_3\) and a precise and clear description of the results of computing \(LZ(L_3)\) and \(TZ(L_3)\) using the definitions to justify this description and justifying the set equality, or (2) a sufficiently general and correct argument why there is no such example, referring back to the relevant definitions.

2. (Graded for correctness) Consider the two regular expressions over \(\Sigma = \{ 0, 1 \}\) \[R_1 = (~(000 \cup 111)^* ~\cup~ (01)^*~) \qquad \qquad R_2 = (~(000)^*(111)^* (\varepsilon \cup 0\cup1))\] You will prove that \[L(R_1) \not \subseteq L(R_2) ~ \text{and} ~ L(R_2) \not \subseteq L(R_1) ~ \text{and} ~ L(R_1) \cap L(R_2) \neq \emptyset ~ \text{and} ~ L(R_1) \cup L(R_2) \neq \Sigma^*\] by giving four example strings that witness these properties.

   1. Specify an example string \(w_1\) such that \(w_1 \in L(R_1) \cap L(R_2)\). Briefly justify your choice, referring to the definitions of the regular expressions and their semantics.

   2. Specify an example string \(w_2\) such that \(w_2 \in L(R_1) \cap \overline{L(R_2)}\). Briefly justify your choice, referring to the definitions of the regular expressions and their semantics.

   3. Specify an example string \(w_3\) such that \(w_3 \in \overline{L(R_1)} \cap L(R_2)\). Briefly justify your choice, referring to the definitions of the regular expressions and their semantics.

   4. Specify an example string \(w_4\) such that \(w_4 \in \overline{L(R_1)} \cap \overline{L(R_2)}\). Briefly justify your choice, referring to the definitions of the regular expressions and their semantics.

3. (Graded for fair effort completeness²)

   1. Pick a four letter alphabet (a nonempty finite set), and specify it, e.g. by filling in the blank \(\Sigma = \underline{\text{fill in your alphabet here}}\).

      Then, pick a language of cardinality (size) \(2\) over this alphabet, and specify it, e.g. by filling in the blank \[L = \underline{\text{fill in your language here}}\] Note: we encourage you to pay attention to syntax here. There are many correct answers; please be precise in how you present the sets you choose.

   2. Give a regular expression that describes the language \(L\) you defined in part (a). Briefly justify why your regular expression works.

   3. Give a DFA that recognizes your language \(L\) you defined in part (a). Specify your DFA both using a formal definition and a state diagram. Briefly justify why your DFA works.

4. (Graded for correctness) Consider the DFA \(C\) given by the state diagram below.

   

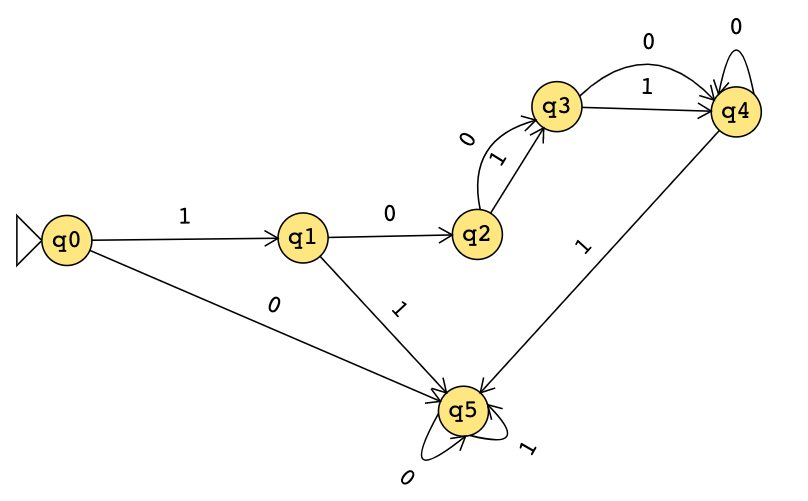
   Suppose someone tells you that the formal definition of this DFA is \[(Q, \Sigma, \delta, q_0, F) = (\{ q0, q1, q2, q3, q4, q5 \}, \{0,1,2\}, \delta, q0, q0)\] where \(\delta: Q \times \Sigma \to Q\) is given by \[\hspace{-1in}\delta ( (q, 0) ) = \begin{cases} q5 & \text{if $q=q0$} \\ qj & \text{if $q=qi$ and $i \in \{1,2,3\}$ and $j=i+1$} \\ q & \text{if $q \in \{q4,q5\}$} \\ \end{cases} \qquad \delta ( (q, 1) ) = \begin{cases} q1 & \text{if $q=q0$} \\ q5 & \text{if $q \in \{q1,q4,q5\}$} \\ \delta( (q,0) ) & \text{if $q=q2$ or $q=q3$} \\ \end{cases}\]

   1. Confirm that this formal description is correct (in that it is consistent with the state diagram), or fix any and all mistakes in it. In your solution, explicitly address whether the description of the set of states is correct, whether the description of the alphabet is correct, whether the description of the transition function is correct, whether the description of the start state is correct, and whether the description of the accept states is correct, and why.

   2. Modify the set of accept states of this state diagram to get a different DFA (with the same set of states, alphabet, start state, and transition function) that recognizes an infinite language. Your solution should include the diagram of this new DFA and an explanation of why the language it recognizes is infinite.

5. (Graded for fair effort completeness) Which of the following are valid descriptions using the terminology we have used in class and in the book so far? For those that aren’t, explain what’s wrong. For those that are, give an example of what’s being described.

   1. A finite automaton accepts a regular expression.

   2. The language described by a regular expression is a finite automaton.

   3. The empty string is the language of some regular expression.

   4. A string of length one uses one symbol from the alphabet.

   5. The input string runs a finite automaton.